
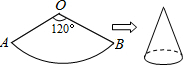
 如图,一个扇形铁皮OAB,已知OA=12cm,∠AOB=120°,小华将OA、OB合拢制成了一个圆锥形烟囱帽(接缝处忽略不计),则烟囱帽的高为8$\sqrt{2}$cm.
如图,一个扇形铁皮OAB,已知OA=12cm,∠AOB=120°,小华将OA、OB合拢制成了一个圆锥形烟囱帽(接缝处忽略不计),则烟囱帽的高为8$\sqrt{2}$cm. 分析 设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2π•r=$\frac{120•π•12}{180}$,解方程求出r,然后利用勾股定理计算所以圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得2π•r=$\frac{120•π•12}{180}$,解得r=4,
所以圆锥的高=$\sqrt{1{2}^{2}-{4}^{2}}$=8$\sqrt{2}$(cm).
故答案为8$\sqrt{2}$cm.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:解答题
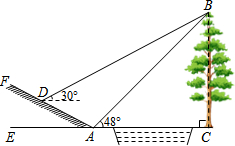 如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)
如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
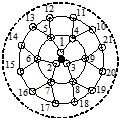 课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为150的微生物会出现在( )
课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为150的微生物会出现在( )| A. | 第3天 | B. | 第4天 | C. | 第5天 | D. | 第6天 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com