
���� ��1�����ݷ�����Ľ����㷽���飬�ɵö�Ԫһ�η����飬������㷨���ɵú���ͼ��
��2�����ݺ���ֵΪ��ʱ���ɵ���Ӧ�Ա�����ֵ��
��3�����������������ʽ���ɵô𰸣�
��� �⣺��1����$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$���뷽����$\left\{\begin{array}{l}{y=ax+6}\\{y=x-b}\end{array}\right.$����$\left\{\begin{array}{l}{2a+6=4}\\{2-b=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$��
����x��y�ķ�����$\left\{\begin{array}{l}{y=-x+6}\\{y=x+2}\end{array}\right.$��
��ͬһֱ������ϵ�ڻ���������������ȷ���ĺ���ͼ��Ϊ��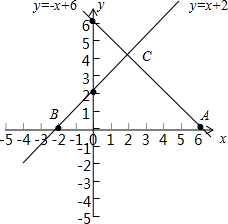 ��
��
��2��y=-x+6����y=0ʱ��-x+6=0�����x�T6����A��6��0����
y=x+2����y=0ʱ��x+2=0�����x=-2����B��-2��0����
��3��������$\left\{\begin{array}{l}{y=-x+6}\\{y=x+2}\end{array}\right.$�Ľ���������C��2��4����
S��ABC=$\frac{1}{2}$��8��4=16��
���� ���⿼����һ�κ������Ԫһ�η����飬������㷨������ͼ���������Ա����뺯��ֵ�Ķ�Ӧ��ϵ�������ε������ʽ���ѷ�����Ľ���뷽����ó���Ԫһ�η������ǽ���ؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
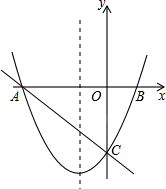 ��ͼ����ֱ������ϵxOy�У�һ�κ���y=-$\frac{2}{3}$x+m��mΪ��������ͼ����x�ύ��A��-3��0������y�ύ�ڵ�C����ֱ��x=-1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬��x�������ύ�ڵ�B��
��ͼ����ֱ������ϵxOy�У�һ�κ���y=-$\frac{2}{3}$x+m��mΪ��������ͼ����x�ύ��A��-3��0������y�ύ�ڵ�C����ֱ��x=-1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬��x�������ύ�ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�DZ߳�Ϊ$\sqrt{3}$�ĵȱ������Σ���P��Q�ֱ�������AB��BC���������㣬��AP=CQ��PQ��AC��D����PE�AAC��E����ôDE�ij���Ϊ$\frac{1}{2}$$\sqrt{3}$��
��ͼ����ABC�DZ߳�Ϊ$\sqrt{3}$�ĵȱ������Σ���P��Q�ֱ�������AB��BC���������㣬��AP=CQ��PQ��AC��D����PE�AAC��E����ôDE�ij���Ϊ$\frac{1}{2}$$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=4x | B�� | $\frac{x}{y}$=-2 | C�� | xy=4 | D�� | y=4x-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com