
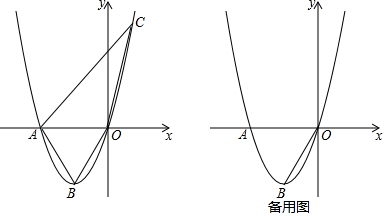
���� ��1����������ת�����Ǻ������B�����꣬�����ô���ϵ�����Ϳ���������κ����Ľ���ʽ��
��2�����ı���ABOC��x��ֳ������Ϊ1��2�������֣��ɵ�S��AOB��S��AOC�ı�ֵΪ1��2��2��1������C��������Ϊ2$\sqrt{3}$��$\frac{\sqrt{3}}{2}$���ٴ����������е�C�����꼴�ɣ�
��3����D������Ϊ��0��y������M��N�����������Ϊ��m��y������n��y������MNΪֱ����Բǡ�þ���ԭ��O�����MON=90�㣬��M��N�ֱ���MF��NE��ֱ��x�ᣬ���MOE�ס�ONF���������������ε����ʿɵ�y2=-m•n����ΪM��N������������߶Գ���x=-1�Գƣ��ɵ�m=-2-n��������ʽ��y2=��2+m��n=n2+2n������N��������������߽���ʽ�ɵ�y=$\sqrt{3}$n2+2$\sqrt{3}$n��Ϊ$\frac{\sqrt{3}}{3}$y=n2+2n���ɵ�y2=$\frac{\sqrt{3}}{3}$y���ⷽ�����D������Ϊ��0��$\frac{\sqrt{3}}{3}$����
��� �⣺��1����OB=OA=2����ת60�㣬
�������Ǻ����ɵ�B��-1��-$\sqrt{3}$����
�������ߵĽ���ʽy=ax2+bx����
$\left\{\begin{array}{l}{4a-2b=0}\\{a-b=-\sqrt{3}}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$��
�������ߵĽ���ʽy=$\sqrt{3}$x2+2$\sqrt{3}$x��
��2�����ı���ABOC��x��ֳ������Ϊ1��2�������֣�
��S��AOB��S��AOC�ı�ֵΪ1��2��2��1��
��C��������Ϊ2$\sqrt{3}$��$\frac{\sqrt{3}}{2}$��
�����������е�C������Ϊ��-1+$\sqrt{3}$��2$\sqrt{3}$������-1-$\sqrt{3}$��2$\sqrt{3}$������-1+$\frac{\sqrt{6}}{2}$��$\frac{\sqrt{3}}{2}$������-1-$\frac{\sqrt{6}}{2}$��$\frac{\sqrt{3}}{2}$����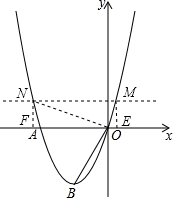 ��3����D������Ϊ��0��y������M��N�����������Ϊ��m��y������n��y����
��3����D��������0��y������M��N�������������m��y������n��y����
��MNΪֱ����Բǡ�þ���ԭ��O�����MON=90�㣬
��M��N�ֱ���MF��NE��ֱ��x�ᣬ
���MOE�ס�ONF��
��$\frac{ME}{OF}$=$\frac{OE}{NF}$����$\frac{y}{-n}$=$\frac{m}{y}$��
��y2=-m•n��
�֡�M��N������������߶Գ���x=-1�Գƣ�
��m+n=-2����m=-2-n��
������ʽ��y2=��2+m��n=n2+2n��
�֡�N��������������߽���ʽ�ɵ�y=$\sqrt{3}$n2+2$\sqrt{3}$n��Ϊ$\frac{\sqrt{3}}{3}$y=n2+2n��
��y2=$\frac{\sqrt{3}}{3}$y��
���y1=0��y2=$\frac{\sqrt{3}}{3}$��
��D��������0��$\frac{\sqrt{3}}{3}$����
���� ���⿼���˶��κ����ۺ��⣬���������ε��ж������ʵ����ã�����ϵ���������Ľ���ʽ�����ã������ε������ʽ�����ã������ʱ��������κ����Ľ���ʽ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
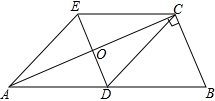
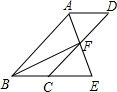 ��ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E������F��AE���е㣬��֤��BF��AF��
��ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E������F��AE���е㣬��֤��BF��AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
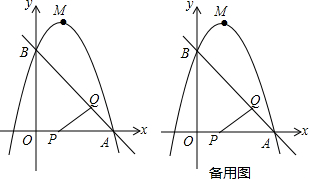
 ��ͼ����Rt��ABC�У���BCA=90�㣬CD��AB���ϵ����ߣ��ֱ����C��D��BA��BC��ƽ���ߣ����߽��ڵ�E����DE��AC�ڵ�O������AE��
��ͼ����Rt��ABC�У���BCA=90�㣬CD��AB���ϵ����ߣ��ֱ����C��D��BA��BC��ƽ���ߣ����߽��ڵ�E����DE��AC�ڵ�O������AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.25��10-5�� | B�� | 25��10-7�� | C�� | 2.5��10-6�� | D�� | 2.5��10-8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
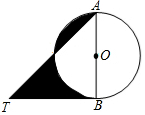 ��ͼ��AB�ǡ�O��ֱ����BT�ǡ�O�����ߣ�����ATB=45�㣬AB=2������Ӱ���ֵ�����ǣ�������
��ͼ��AB�ǡ�O��ֱ����BT�ǡ�O�����ߣ�����ATB=45�㣬AB=2������Ӱ���ֵ�����ǣ�������| A�� | 2 | B�� | $\frac{3}{2}$-$\frac{1}{4}$�� | C�� | 1 | D�� | $\frac{1}{2}$+$\frac{1}{4}$�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com