
 在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.分析 ①有三种情况是真命题:情况一:由AAS证明△ABC≌△DEF,得出对应边相等BC=EF,即可得出BF=EC;
情况二:先证BC=EF,由SAS证明△ABC≌△DEF,即可得出∠1=∠2;
情况三:先证出BC=EF,再由ASA证明△ABC≌△DEF,即可得出AB=DE;
②先证BC=EF,由SAS证明△ABC≌△DEF,即可得出∠1=∠2.
解答 解:①情况一:题设:①②④;结论:③;
情况二:题设①③④;结论:②;
情况三:题设②③④;结论:①.
②选择的题设:①③④;结论:②;
理由::∵BF=EC,
∴BF+CF=EC+CF,即BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}&{\;}\\{∠B=∠E}&{\;}\\{BC=EF}&{\;}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴∠1=∠2;
故答案为:①③④;②.
点评 本题考查了全等三角形的判定与性质以及命题与定理;熟练掌握全等三角形的判定方法证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
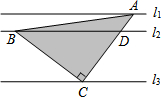 直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为( )
直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为( )| A. | $\frac{25}{4}$ | B. | $\frac{25}{2}$ | C. | 12 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿C-A-B向点B以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当P点到达C点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿C-A-B向点B以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当P点到达C点时,另一点也随之停止运动,设运动时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,点B为⊙O上一点,满足BC∥OP.
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,点B为⊙O上一点,满足BC∥OP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 78分 | B. | 86分 | C. | 80分 | D. | 82分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20、15 | B. | 15、20 | C. | 25、10 | D. | 10、25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com