
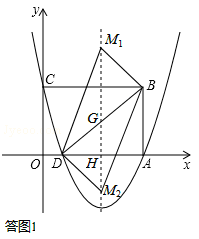
 经过A、C两点,与x轴的另一个交点是点D,连接BD.
经过A、C两点,与x轴的另一个交点是点D,连接BD.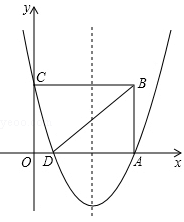
 上,
上,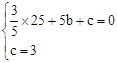 ,解得:
,解得: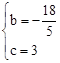 。
。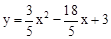 。
。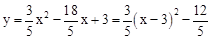 ,
,
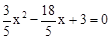 ,解得x=1或x=5。
,解得x=1或x=5。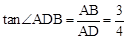 ,∴GH=DH•tan∠ADB=2×
,∴GH=DH•tan∠ADB=2×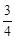 =
=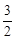 。
。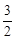 )。
)。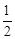 MG•DH+
MG•DH+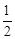 MG•AH=6,即:
MG•AH=6,即: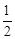 MG×2+
MG×2+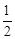 MG×2=6。
MG×2=6。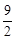 )或(3,
)或(3, )。
)。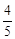 ,cosB=
,cosB= 。
。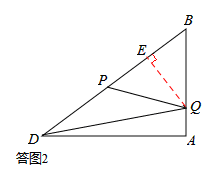
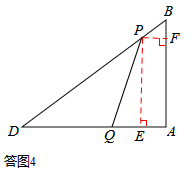
 t,QE=BQ•sinB=
t,QE=BQ•sinB=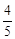 t,
t, t=
t=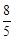 t。
t。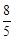 t)2+(
t)2+(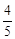 t)2=42+(3﹣t)2,整理得:11t2+6t﹣25=0,
t)2=42+(3﹣t)2,整理得:11t2+6t﹣25=0, 或t=﹣5(舍去)。
或t=﹣5(舍去)。 。
。
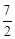 。
。
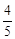 =4﹣
=4﹣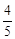 t,BF=PB•cosB=(5﹣t)×
t,BF=PB•cosB=(5﹣t)× =3﹣
=3﹣ t。
t。 t)=
t)= t。
t。 t,AE=PF=4﹣
t,AE=PF=4﹣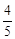 t。∴EQ=AQ﹣AE=(t﹣3)﹣(4﹣
t。∴EQ=AQ﹣AE=(t﹣3)﹣(4﹣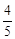 t)=
t)=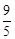 t﹣7。
t﹣7。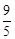 t﹣7)2+(
t﹣7)2+( t)2=(7﹣t)2,
t)2=(7﹣t)2, 。
。 。
。 或t=
或t=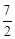 或t=
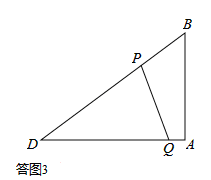
或t= 时,以D、P、Q为顶点的三角形是等腰三角形。
时,以D、P、Q为顶点的三角形是等腰三角形。

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变)。
的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变)。 上任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到
上任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到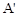 (
(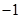 ,3),再向下平移2个单位得到
,3),再向下平移2个单位得到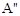 (
(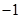 ,1);点B向左平移1个单位得到
,1);点B向左平移1个单位得到 (0,4),再向下平移2个单位得到
(0,4),再向下平移2个单位得到 (0,2)。
(0,2)。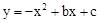 。
。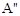 (
(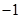 ,1),
,1), (0,2)在抛物线上。
(0,2)在抛物线上。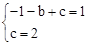 ,解得:
,解得: 。
。 。
。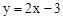 向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式。
向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
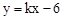 与抛物线
与抛物线 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。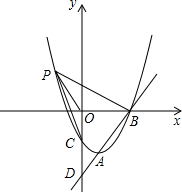
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过A,B,C三点,顶点为F.
经过A,B,C三点,顶点为F.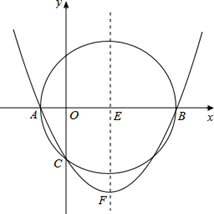
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com