练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    设2+
    		6
    的整数部分和小数部分分别是x、y，请求x、y的值，并确定x与y的正负性．
    考点：估算无理数的大小
    专题：
    分析：先求出
    		6
    的范围，再求出2+
    		6
    的范围，即可得出答案．
    解答：解：∵2＜
    		6
    ＜3，
    ∴都加上2得：4＜2+
    		6
    ＜5，
    ∴x=4，y=2+
    		6
    -4=
    		6
    -2，
    ∴x＞0，y＞0．
    点评：本题考查了估算无理数的大小的应用，关键是求出2+
    		6
    的范围．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    根据如图所示的某函数的图象，回答下列问题，
    （1）自变量x的取值范围是
     
    ；
    （2）当x=2时，y=
     
    ，当x=
     
    时，y=4；
    （3）函数的图象与x轴的交点坐标是
     
    ；与y轴的交点坐标是
     
    ；若y随x的增大而减小，则x的取值范围是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在2012年某校初中毕业体育考试中，考生人数共为800人，为了解考试成绩情况，从中抽取了部分学生的成绩统计进行了统计，请你根据下面尚未完成的频数、频率分布表分布直方图，解答下列问题：
    分组 频数 频率
    51～60 1 0.02
    61～70 6
     
    71～80 12 0.24
    81～90 18 0.36
    91～101
     
     
    合计 50
     
    注意：51～60表示大于等于51小于60
    （1）填写频数频率分布表中的空格；
    （2）本次抽取学生人数是多少？
    （3）哪个范围内的学生人数最多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我市某公司要将一批105吨的物资运往外地，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
    车型 甲 乙 丙
    汽车运载量（吨/辆） 5 8 10
    汽车运费（元/辆） 400 500 600
    （1）若全部物资都用甲、乙两种车型来运送，需运费7700元，问分别需甲、乙两种车型各几辆？
    （2）若该公司打算用甲、乙、丙三种车型同时参与运送，已知它们的总辆数为13辆，你能分别求出三种车型的辆数吗？此时的运费又是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知a、b、c在数轴上的位置如图，试求|a+b|+|b|+|-c|的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，已知⊙O的半径是2，C为直径BA延长线上一点，OC=4，过C作直线CF使∠OCF=30°．
    （1）求证：⊙O与直线CF相切；
    （2）如图2，设（1）中的切点为E，Q为圆周上一点，EQ交AB于D，cos∠AEQ=
    3
    4
    ，求
    BD
    DE
    的值；
    （3）如图3，设P为线段AC上的一个动点（不与A、C重合），求证：不论P在何处，总存在弦EQ（EQ与AB交于D）使得ED•QD=AP•PC成立．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某市为了了解“五一”期间该县常住居民出游情况，有关部门随即调查了1600名常住居民，并根据调查结果绘制了如下统计图

    根据以上信息，解答下列各题：
    （1）补全条形信息统计图．
    （2）在扇形统计图中，出游的主要目的是采集发展信息所对应的圆心角的度数为多少？
    （3）若该市常住居民24万人，请估计出游的主要目的是采集发展信息的人数．

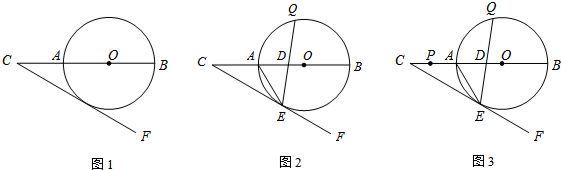
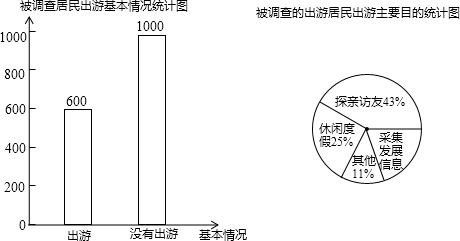
    查看答案和解析>>

    科目：初中数学 来源： 题型：

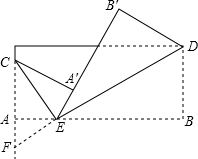    如图，将长方形纸片的两角分别折叠，使顶点B落在B′处，顶点A落在A′处，EC为折痕，点E、A′、B′在同一条直线上．
    （1）猜想折痕EC和ED的位置关系，并说明理由．
    （2）ED的反向延长线交CA交于F，若∠BED=35°，求∠AEF和∠A′EC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）+14-10-（-9）+（-5）
    （2）-
    1
    2
    -
    5
    4
    -（-
    3
    2
    ）+（-
    1
    4
    ）
    （3）-18+（-7.5）-（-31）-12.5
    （4）（
    1
    2
    +
    5
    6
    -
    7
    12
    ）×（-36）

    查看答案和解析>>

    同步练习册答案