
分析 (1)因为佛山移动公司手机资费两种套餐:A套餐:月租0元,市话通话费每分钟0.49元;B套餐:月租费48元,免费市话通话时间48分钟,超出部分每分钟0.25元,两种方式的费用分别为y1元和y2元,则y1=0.49x,y2=48+0.25x;
(2)令y1=y2,解方程即可;
(3)根据(2)的结果即可求解.
解答 解:(1)y1=0.49x,
y2=48+0.25x;
(2)令y1=y2,则0.49x=48+0.25x,
解得x=200.
故月市话通话时间为200分钟长时,两种套餐收费一样;
(3)∵月市话通话时间为200分钟长时,两种套餐收费一样,
∴小明爸爸每月市话通话时间为200分钟,选择两种套餐一样合算.
点评 此题主要考查了一次函数的应用,需仔细分析题意,建立函数解析式,利用方程或简单计算即可解决问题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠A=36°,线段AB=6.
如图,已知∠A=36°,线段AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
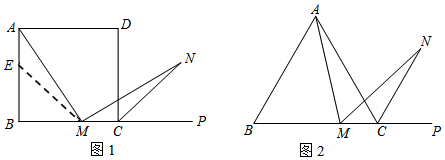
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com