
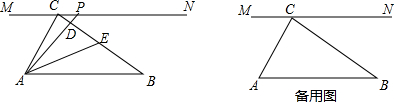
分析 (1)先由勾股定理求BC,再根据平行相似得比例式$\frac{CP}{AB}=\frac{CD}{BD}$,得CD=$\frac{2}{3}$;
(2)延长AE交MN于F,构建相似三角形,设AE=BE=a,利用勾股定理列等式求出AE和CE的长,作辅助线EG,根据计算EG的长与EC的长作对比可知:P不在射线CN上,则当P在射线CM上时,通过证明△CFE∽△BAE得比例式$\frac{CF}{AB}=\frac{CE}{BE}$,并将各线段的值代入得出y关于x的函数关系式;
(3)当△AEP是直角三角形时,分两种情况讨论:①当∠AEP=90°时,作AG⊥MN于G,证明△CEF≌△BEA得CF=AB,即y+x=5;根据△ACG∽△BAC,得AG=$\frac{12}{5}$,CG=$\frac{9}{5}$,FG=$\frac{34}{5}$;再利用勾股定理求出结论;
②当∠APE=90°时,作EH⊥AB于H,证明△PDE∽△CDA和△CDP∽△ADE,求出AH=$\frac{5}{2}$,则AP=AH=$\frac{5}{2}$,由
y=-x+$\frac{7}{5}$求出x的值并取舍;最后写出结论.
解答 解:在Rt△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4
(1)∵MN∥AB,
∴△CPD∽△ABD,
∴$\frac{CP}{AB}=\frac{CD}{BD}$
∵CP=1,AB=5,BC=4,
∴$\frac{1}{5}=\frac{CD}{4-CD}$,解得CD=$\frac{2}{3}$;
(2)过E作EG⊥AB于G,如图1,
∵AE=BE,
∴∠EAB=∠EBA,
∴AG=BG,
tan∠ABC=$\frac{AC}{BC}=\frac{EG}{BG}$=$\frac{3}{4}$,
设EG=3x,则AG=BG=4x,
∴8x=5,
x=$\frac{5}{8}$,
∴EG=3×$\frac{5}{8}$=$\frac{15}{8}$,
延长AE交MN于F,如图2,
∵MN∥AB,
∴∠PFA=∠FAB.
∵∠PAE=∠FAB,
∴∠PAE=∠PFA,
∴PF=PA=y.
∵△ABE是等腰三角形,
∴AE=BE.设AE=BE=a,则CE=4-a.
∵AE2=AC2+CE2,
∴a2=32+(4-a)2,解得a=$\frac{25}{8}$,即BE=$\frac{25}{8}$,CE=$\frac{7}{8}$,
∵MN∥AB,
∴△CFE∽△BAE,
∴$\frac{CF}{AB}=\frac{CE}{BE}$.
∵AC⊥EC,EC=$\frac{7}{8}$$<\frac{15}{8}$,
∴当P不可能在射线CN上,
∴当P在射线CM上时(如图2),CF=y-x,
∴$\frac{y-x}{5}=\frac{\frac{7}{8}}{\frac{25}{8}}$,y=x+$\frac{7}{5}$;
(3)如图3,连结PE.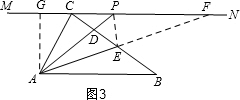
①当∠AEP=90°时,作AG⊥MN于G,
∵PA=PF,
∴AE=EF,
又∠CEF=∠BEA,∠CFE=∠BAE,
∴△CEF≌△BEA,
∴CF=AB,即y+x=5,
∵△ACG∽△BAC,
∴$\frac{AG}{BC}=\frac{CG}{AC}=\frac{AC}{AB}$,即$\frac{AG}{4}=\frac{CG}{3}=\frac{3}{5}$,
∴AG=$\frac{12}{5}$,CG=$\frac{9}{5}$,FG=$\frac{34}{5}$,
∵AG2+PG2=AP2,
∴$(\frac{12}{5})^{2}+(\frac{34}{5}-y)^{2}={y}^{2}$,
解得y=$\frac{65}{17}$,
∴x=5-y=$\frac{20}{17}$,即CP=$\frac{20}{17}$;
②如图4,当∠APE=90°时,作EH⊥AB于H,
∵∠APE=∠ACD,∠PDE=∠CDA,
∴△PDE∽△CDA,
∴$\frac{PD}{DE}=\frac{CD}{AD}$,
又∠CDP=∠ADE,
∴△CDP∽△ADE,
∴∠PCD=∠PAE,
∵∠PCD=∠B,∠PAE=∠BAE,
∴∠B=∠BAE,
∴AE=BE,
∴AH=BH=$\frac{1}{2}$AB=$\frac{5}{2}$,
同(2)中①,得y=-x+$\frac{7}{5}$,而y=AP=AH=$\frac{5}{2}$,
∴CP=x=$\frac{7}{5}$-$\frac{5}{2}$<0,舍去;
综上所述,△AEP是直角三角形时,CP=$\frac{20}{17}$.
点评 本题是三角形的综合题,考查了相似三角形、等腰三角形和勾股定理的性质和应用,利用相似三角形的比例式及勾股定理列等式求边长;如果一个三角形是直角三角形,不确定哪一个角是直角的情况下要采取分类讨论的方法解决.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:选择题
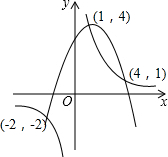 二次函数y=ax2+bx+c(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交(如图),则不等式ax2+bx+c>$\frac{k}{x}$的解集是( )
二次函数y=ax2+bx+c(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交(如图),则不等式ax2+bx+c>$\frac{k}{x}$的解集是( )| A. | 1<x<4或x<-2 | B. | 1<x<4或-2<x<0 | ||
| C. | 0<x<1或x>4或-2<x<0 | D. | -2<x<1或x>-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
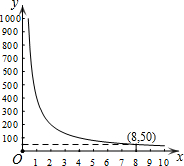 码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图.
码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点M,N分别是BC,CD边上的点,连接AM,BN,若BM=CN.
如图,在正方形ABCD中,点M,N分别是BC,CD边上的点,连接AM,BN,若BM=CN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com