
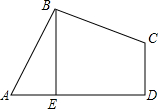
 如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE=( )
如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 运用割补法把原四边形转化为正方形,求出BE的长.
解答 解:如图,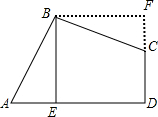
过B点作BF⊥CD,与DC的延长线交于F点,
∵∠ABC=∠CDA=90°,BE⊥AD,
∴四边形EDFB是矩形,∠EBF=90°,
∴∠ABE=∠CBF,
∵在△BCF和△BAE中,
$\left\{\begin{array}{l}{∠F=∠BEA}\\{∠CBF=∠ABE}\\{AB=BC}\end{array}\right.$
∴△BCF≌△BAE(ASA),
∴BE=BF,
∴四边形EDFB是正方形,
∴S四边形ABCD=S正方形BEDF=4,
∴BE=$\sqrt{4}$=2.
故选:B.
点评 此题考查三角形全等的判定与性质,正方形的判定与性质,运用割补法把原四边形转化为正方形,其面积保持不变,所求BE就是正方形的边长了;也可以看作将三角形ABE绕B点逆时针旋转90°后的图形.


科目:初中数学 来源: 题型:解答题
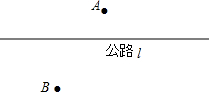 如图所示,A,B两村在公路l的两旁,现需在公路上修建一个汽车站,使车站到两村的距离相等,你能在公路l上确定这个车站的位置吗?(尺规作图作出P点的位置,不写作法,保留作图痕迹,写出结论)
如图所示,A,B两村在公路l的两旁,现需在公路上修建一个汽车站,使车站到两村的距离相等,你能在公路l上确定这个车站的位置吗?(尺规作图作出P点的位置,不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{6}$m | B. | $\frac{23}{6}$m | C. | $\frac{6}{25}$m | D. | $\frac{5}{2}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com