
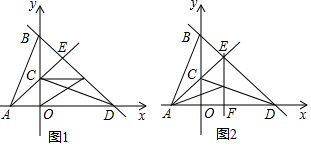
ЗжЮі ЃЈ1ЃЉгЩAЁЂBЕФзјБъПЩЧѓЕУAOКЭOBЕФГЄЃЌгЩа§зЊЕФаджЪПЩЧѓЕУOCЁЂODЕФГЄЃЌДгЖјПЩЧѓЕУЁЯAEB=90ЁуЃЌдйгЩЙДЙЩЖЈРэПЩЧѓЕУCDКЭABЕФГЄЃЌПЩЧѓЕУAB=CDЃЌПЩжЄЕУЁїABEЁеЁїDCEЃЛ
ЃЈ2ЃЉгЩBЁЂDзјБъПЩЧѓЕУжБЯпBDНтЮіЪНЃЌЕБMЕудкxжсЩЯЗНЪБЃЌдђгаCMЁЮANЃЌдђПЩЧѓЕУMЕузнзјБъЃЌДњШыжБЯпBDНтЮіЪНПЩЧѓЕУMЕузјБъЃЌЕБMЕудкxжсЯТЗНЪБЃЌЭЌРэПЩЧѓЕУMЕузнзјБъЃЌдђПЩЧѓЕУMЕузјБъЃЛ
ЃЈ3ЃЉгЩAE=DEПЩжЊAЁЂDЙигкEFЖдГЦЃЌСЌНгCDНЛEFгкЕуPЃЌдђPЕуМДЮЊТњзуЬѕМўЕФЕуЃЌгЩCЁЂDзјБъПЩЧѓЕУжБЯпCDЕФНтЮіЪНЃЌдђПЩЧѓЕУPЕузјБъЃЌРћгУЙДЙЩЖЈРэПЩЗжБ№ЧѓЕУACКЭCDЕФГЄЃЌдђПЩЧѓЕУДЫЪБЁїPACЕФжмГЄЃЎ
НтД№ НтЃК
ЃЈ1ЃЉЁпAЃЈ-2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌ
ЁрOA=2ЃЌOB=4ЃЌ
ЁпНЋЁїOABШЦOЕуЫГЪБеыа§зЊ90ЁуЕУЁїOCDЃЌ
ЁрOC=OA=2ЃЌOD=OB=4ЃЌAB=CDЃЌ
ЁрЁЯACO=ЁЯACE=ЁЯCBE=45ЁуЃЌ
ЁрЁЯCEB=90ЁуЃЌ
ЁрЁЯAEB=ЁЯCEDЃЌЧвCE=BEЃЌ
дкRtЁїABEКЭRtЁїDCEжа
$\left\{\begin{array}{l}{AB=CD}\\{BE=CE}\end{array}\right.$
ЁрRtЁїABEЁеRtЁїDCEЃЈHLЃЉЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊDЃЈ4ЃЌ0ЃЉЃЌЧвBЃЈ0ЃЌ4ЃЉЃЌ
ЁржБЯпBDНтЮіЪНЮЊy=-x+4ЃЌ
ЕБMЕудкxжсЩЯЗНЪБЃЌдђгаCMЁЮANЃЌМДCMЁЮxжсЃЌ
ЁрMЕуЕНxжсЕФОрРыЕШгкCЕуЕНxжсЕФОрРыЃЌ
ЁрMЕуЕФзнзјБъЮЊ2ЃЌ
дкy=-x+4жаЃЌСюy=2ПЩЕУx=2ЃЌ
ЁрMЃЈ2ЃЌ2ЃЉЃЛ
ЕБMЕудкxжсЯТЗНЪБЃЌЭЌРэПЩЕУMЕуЕФзнзјБъЮЊ-2ЃЌ
дкy=-x+4жаЃЌСюy=-2ПЩЧѓЕУx=6ЃЌ
ЁрMЕуЕФзјБъЮЊЃЈ6ЃЌ-2ЃЉЃЛ
злЩЯПЩжЊMЕуЕФзјБъЮЊЃЈ2ЃЌ2ЃЉЛђЃЈ6ЃЌ-2ЃЉЃЛ
ЃЈ3ЃЉгЩЃЈ1ЃЉПЩжЊAE=CEЃЌ
ЁрAЁЂDЙигкжБЯпEFЖдГЦЃЌ
СЌНгCDНЛEFгкЕуPЃЌдђPA=PDЃЌ
ЁрPA+PC=PD+PC=CDЃЌ
ЁрТњзуЁїPACЕФжмГЄзюаЁЃЌ
ЁпCЃЈ0ЃЌ2ЃЉЃЌDЃЈ4ЃЌ0ЃЉЃЌ
ЁрПЩЩшжБЯпCDНтЮіЪНЮЊy=kx+2ЃЌ
Ёр4k+2=0ЃЌНтЕУk=-$\frac{1}{2}$ЃЌ
ЁржБЯпCDНтЮіЪНЮЊy=-$\frac{1}{2}$x+2ЃЌ
ЁпAЃЈ-2ЃЌ0ЃЉЃЌDЃЈ4ЃЌ0ЃЉЃЌ
ЁрFЃЈ1ЃЌ0ЃЉЃЌМДжБЯпEFНтЮіЪНЮЊx=1ЃЌ
дкy=-$\frac{1}{2}$x+2жаЃЌСюx=1ПЩЕУy=$\frac{3}{2}$ЃЌ
ЁрPЃЈ1ЃЌ$\frac{3}{2}$ЃЉЃЌ
дкRtЁїAOCжаЃЌгЩЙДЙЩЖЈРэПЩЧѓЕУAC=2$\sqrt{2}$ЃЌ
дкRtЁїCODжаЃЌгЩЙДЙЩЖЈРэПЩЧѓЕУCD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$ЃЌ
ЁрPA+PC+AC=CD+AC=2$\sqrt{5}$+2$\sqrt{2}$ЃЌ
МДЁїPACЕФжмГЄзюаЁжЕЮЊ2$\sqrt{5}$+2$\sqrt{2}$ЃЎ
ЕуЦР БОЬтЮЊвЛДЮКЏЪ§ЕФзлКЯгІгУЃЌЩцМАа§зЊЕФаджЪЁЂЕШбќжБНЧШ§НЧаЮЕФХаЖЈКЭаджЪЁЂШЋЕШШ§НЧаЮЕФХаЖЈКЭаджЪЁЂЦНааЫФБпаЮЕФаджЪЁЂжсЖдГЦЕФаджЪЕШжЊЪЖЃЎдкЃЈ1ЃЉжажЄЕУЁЯAEB=90ЁуЪЧНтЬтЕФЙиМќЃЌдкЃЈ2ЃЉжаЧѓЕУMЕуЕФзнзјБъЪЧНтЬтЕФЙиМќЃЌдкЃЈ3ЃЉжаШЗЖЈГіPЕуЕФЮЛжУЪЧНтЬтЕФЙиМќЃЎБОЬтПМВщжЊЪЖЕуНЯЖрЃЌзлКЯадНЯЧПЃЌФбЖШЪЪжаЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
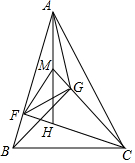 ШчЭМЃЌЁїABCЮЊШёНЧШ§НЧаЮЃЌCFЁЭABгкFЃЌHЮЊЁїABCЕФДЙаФЃЎMЮЊAHЕФжаЕуЃЌЕуGдкЯпЖЮCMЩЯЃЌЧвCGЁЭGBЃЎ
ШчЭМЃЌЁїABCЮЊШёНЧШ§НЧаЮЃЌCFЁЭABгкFЃЌHЮЊЁїABCЕФДЙаФЃЎMЮЊAHЕФжаЕуЃЌЕуGдкЯпЖЮCMЩЯЃЌЧвCGЁЭGBЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com