
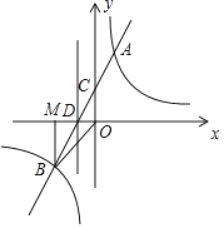
����Ŀ����ͼ��һ�κ���y��mx+n��m��0����ͼ���뷴��������y��![]() ��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����Ϊ��M��BM��OM��2����A��������Ϊ4��
��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����Ϊ��M��BM��OM��2����A��������Ϊ4��
��1����÷�����������һ�κ����ı���ʽ��
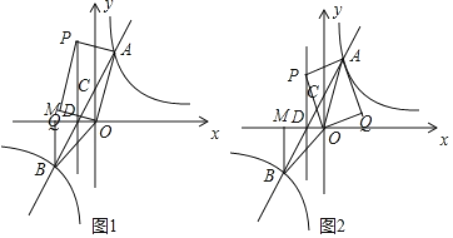
��2��ֱ��AB��x���ڵ�D������D��ֱ��l��x�ᣬ���ֱ��l�ϴ��ڵ�P������ƽ���ڴ��ڵ�Q��ʹ�ı���OPAQ�Ǿ��Σ������P�����꣮
���𰸡���1��y��![]() ��y��2x+2����2�����ڣ�����1��
��y��2x+2����2�����ڣ�����1��![]() ����1��2+
����1��2+![]() ����1��2��
����1��2��![]() ����
����
��������
��1����������ó�B�����꣬�����ó���������������ʽ�������ô���ϵ�����ó�һ�κ�������ʽ��
��2����P��-1��a������ͼ1������PAO=90������ͼ2������APO=90�������ݹ��ɶ����з��̼��ɵõ����ۣ�
�⣺��1����BM��OM��2��
���B����������2����2����
�跴���������Ľ���ʽΪy��![]() ��
��
��2��![]() ��
��
��k��4��
�෴���������Ľ���ʽΪy��![]() ��
��
�ߵ�A����������4��
��4��![]() ��
��
��x��1��
���A��������1��4����
��һ�κ���y��mx+n��m��0����ͼ�����A��1��4������B����2����2����
��![]() ��
��
��ã�![]() ��
��
��һ�κ����Ľ���ʽΪy��2x+2��
��2�����ڣ�
��ֱ��AB��x�ύ��D��
��D����1��0����
��OD��1��
��P����1��a����
��ͼ1������PAO��90����
��OP2��PA2+OA2��PD2+OD2��
�ࣨ1+1��2+��4��a��2+12+42��12+a2��
��ã�a��![]() ��
��
��P����1��![]() ����
����
��ͼ2������APO��90����
��OP2��OA2��PA2��PD2+OD2��
��12+42��[��1+1��2+��4��a��2]��12+a2��
��ã�a��2��![]() ��
��
��P����1��2+![]() ����1��2��
����1��2��![]() ����
����
������������P����������1��![]() ����1��2+
����1��2+![]() ����1��2��
����1��2��![]() ����
����
�ʴ�Ϊ����1��y��![]() ��y��2x+2����2�����ڣ�����1��
��y��2x+2����2�����ڣ�����1��![]() ����1��2+
����1��2+![]() ����1��2��
����1��2��![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������![]() ��x��0����ͼ����A��2����1����B��
��x��0����ͼ����A��2����1����B��![]() ��n�����㣬ֱ��y=2��y�ύ�ڵ�C��
��n�����㣬ֱ��y=2��y�ύ�ڵ�C��

��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��
��1����ͼ�٣���������ABCD�ڣ��뻭��ʹ��BPC=90�������е�P��
��2����ͼ�ڣ���֪����ABCD��AB=9��BC=10���ھ���ABCD��(����)����ʹ��BPC=60�������е�P���������APD��������ֵ��
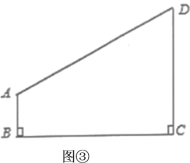
��3��������ᷢչ��ũҵ�۹��߽������ǵ����ijũҵ�۹���ƽ��ʾ��ͼ��ͼ3��ʾ���ı���ABCD�����С�A=120������B=��C=90����AB=![]() km��BC=6km���۹����������������һ��P��ʹ�õ�P���A��B��C��D�����ӵ��߶ν������۹��ֳ��ĸ������������в�ͬ�������滮����ʵ�ú����۵ĽǶ����ǻ�Ҫ������BPC�������ڡ�BPC=120��������APD�����������С���������ı���ABCD���Ƿ���������ĵ�P��ʹ�á�BPC=120��������APD�����С�������ڣ�������ͼ�л�����P���λ�ã��������APD����С���.�������ڣ�˵������.
km��BC=6km���۹����������������һ��P��ʹ�õ�P���A��B��C��D�����ӵ��߶ν������۹��ֳ��ĸ������������в�ͬ�������滮����ʵ�ú����۵ĽǶ����ǻ�Ҫ������BPC�������ڡ�BPC=120��������APD�����������С���������ı���ABCD���Ƿ���������ĵ�P��ʹ�á�BPC=120��������APD�����С�������ڣ�������ͼ�л�����P���λ�ã��������APD����С���.�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx��c��ͼ���㣨2��-5������������Ϊ��-1��4����ֱ��l�Ľ���ʽΪy=2x+m.
��1���������ߵĽ���ʽ��
��2������������ֱ��l�����������㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����ֱ��l��������ֻ��һ��������P�����P�����ꣻ
��4������������![]() ��Ľ���ֱ�ΪA��B�����ڣ�3���������¡�PAB�����.
��Ľ���ֱ�ΪA��B�����ڣ�3���������¡�PAB�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ��㶼��С����ĸ���ϣ�
��1����A�������� ����C�������� ��
��2����ԭ��OΪλ�����ģ�����ABC��С��ʹ�任��õ��ġ�A1B1C1���ABC��Ӧ�ߵı�Ϊ1��2�����������л�����A1B1C1��
��3����A1B1C1�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԫ���ڼ䣬ij������50�����乩�ο;�ס����ÿ������ÿ��Ķ���Ϊ180Ԫʱ�������ȫ��ס������ÿ������ÿ��Ķ���ÿ����10Ԫʱ���ͻ���һ��������У�����ο;�ס���䣬�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã�
��1�������۶�Ϊ200Ԫʱ�������ÿ�������
��2�����۶�Ϊ����ʱ������ÿ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ��
��ͼ����һ�κ���y=x+b��ͼ��
�ڵ�A��1��4������B��-4��n����

��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
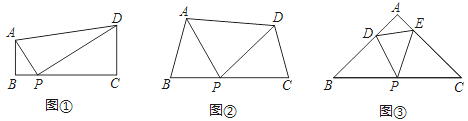
����Ŀ����֪����ͼ�������ı���ABCD�У�AB��CD����B=90�㣬��P��BC���ϣ�����APD=90��ʱ����֪��ABP�ס�PCD������Ҫ��֤����
̽������ͼ�������ı���ABCD�У���P��BC���ϣ�����B=��C=��APDʱ����֤����ABP�ס�PCD��
��չ����ͼ��������ABC�У���P�DZ�BC���е㣬��D��E�ֱ��ڱ�AB��AC�ϣ�����B=��C=��DPE=45�㣬BC=6![]() ��CE=4����DE�ij�Ϊ�� ����
��CE=4����DE�ij��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������50�����乩�ο;�ס����ÿ�����䶨��120Ԫʱ�������ȫ��ס������ÿ������ÿ��Ķ���ÿ����10Ԫʱ���ͻ���һ��������У�����ο;�ס���䣬�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã���ÿ�����䶨��ΪxԪ��xΪ��������
��1��ֱ��д��ÿ���ο;�ס�ķ�������y��x�ĺ�������ʽ��
��2�������ÿ�������ΪWԪ����ÿ�䷿�۶���Ϊ����Ԫʱ������ÿ���������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com