
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.

【答案】(1)见解析;(2)①3;②45.
【解析】
(1)证出EC为⊙O的切线;由切线长定理得出EC=ED,再求得EB=ED,即可得出结论;
(2)①由含30°角的直角三角形的性质得出AB,由勾股定理求出BC,再由直角三角形斜边上的中线性质即可得出DE;
②由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
(1)证明:连接DO.
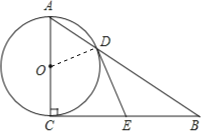
∵∠ACB=90°,AC为直径,
∴EC为⊙O的切线;
又∵ED也为⊙O的切线,
∴EC=ED,
又∵∠EDO=90°,
∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°
又∵∠B+∠A=90°,
∴∠BDE=∠B,
∴BE=ED,
∴BE=EC;
(2)解:①∵∠ACB=90°,∠B=30°,AC=2![]() ,
,
∴AB=2AC=4![]() ,
,
∴BC=![]() =6,
=6,
∵AC为直径,
∴∠BDC=∠ADC=90°,
由(1)得:BE=EC,
∴DE=![]() BC=3,
BC=3,
故答案为:3;
②当∠B=45°时,四边形ODEC是正方形,理由如下:
∵∠ACB=90°,
∴∠A=45°,
∵OA=OD,
∴∠ADO=45°,
∴∠AOD=90°,
∴∠DOC=90°,
∵∠ODE=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴矩形DECO是正方形.
故答案为:45.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数 y=-2x+4,完成下列问题:

(1)在所给直角坐标系中画出此函数的图象;
(2)根据图象回答:当 x 时,y>2.
(3)求出函数图象与坐标轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC,P点在BC边上的高AD上,且![]() ,BP的延长线交AC于E,若S△ABC=10,则S△ABE=_____;S△DEC=_____.
,BP的延长线交AC于E,若S△ABC=10,则S△ABE=_____;S△DEC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若∠APC=3∠BPC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(x,0),B(0,y),且x,y满足![]() ,且点A与点C关于y轴对称.
,且点A与点C关于y轴对称.
(1)求C坐标;
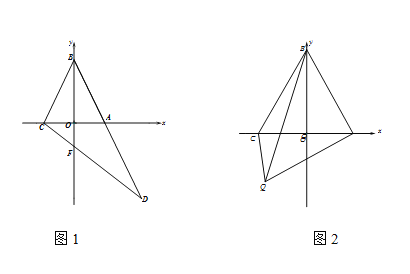
(2)如图1,点D在射线BA上,连接CD,若b=4,∠D=![]() ∠CBA,求CD长
∠CBA,求CD长
(3)如图2,如图2,BC=2OC,点Q是平面内一点,连接 QB,QC,QA,若QB=m,QC=OA,求AQ最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com