练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    课本上，公式 (a－b)2＝a2－2ab＋b2 是由公式 (a＋b)2＝a2＋2ab＋b2 推导得出的．

    已知 (a＋b)4＝a4＋4a3b＋6a2b2＋4ab3＋b4，则 (a－b)4＝       ．


    a4－4a3b＋6a2b2－4ab3＋b4   

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


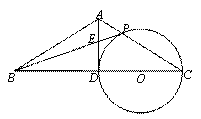
    已知：如图，在△ABC中，AB=AC，点D是边BC的中点．以

    CD为直径作⊙O，交边AC于点P，连接BP，交AD于点E．

    （1）求证：AD是⊙O的切线；

    （2）如果PB是⊙O的切线，BC=4，求PE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在□ABCD中，∠A＝70° ，将□ABCD绕顶点B顺时针旋转到□A1BC1D1，当C1D1首次经过顶点C时，旋转角∠ABA1＝          °．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示的平面图形能折叠成的长方体是

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的一元二次方程3(x－1)(x－m)＝0的两个根是1和2，则m的值是       ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


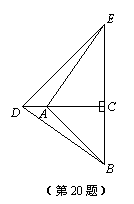
    如图，在△ABC和△CDE中，∠ACB＝∠DCE＝90°，AC＝BC，DC＝EC，且点A在CD上，连接AE、BD．

    （1）求证：AE＝BD；

    （2）若AB＝CD，将△ABC绕点C逆时针旋转一周，当以A、B、C、D为顶点的四边形是平行四边形时，直接写出旋转角的度数．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果两个多边形不仅相似（相似比不等于1），而且有一条公共边，那么就称这两个多边形是共边相似多边形．例如，图①中，△ABC与△ACD是共AC边相似三角形，图②中，□ABCD与□CEFD是共CD边相似四边形．

     


    （1）判断下列命题的真假（在相应括号内填上“真”或“假”）：

    ①正三角形的共边相似三角形是正三角形．（   ）

    ②如果两个三角形是位似三角形，那么这两个三角形不可能是共边相似三角形．（   ）

    （2）如图③，在△ABC中，∠C＝90°，∠A＝50°，画2个不全等的三角形，使这2个三角形均是与△ABC共BC边的相似三角形．（要求：画图工具不限，不写画法，保留画图痕迹或有必要的说明）

         （3）图④是相邻两边长分别为a、b（a＞b）的矩形，图⑤是边长为c的菱形，图⑥是两底长分别为d、e，腰长为f（0＜e－d＜2f）的等腰梯形，判断这三个图形是否存在共边相似四边形？如果存在，直接写出它们的共边相似四边形各边的长度．

     


         （4）根据（1）、（2）和（3）中获得的经验回答：如果一个多边形存在它的共边相似多边形，那么它必须满足条件：     ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


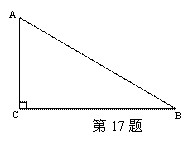
    ）如图，在△ABC中，∠C=90°，∠B=30°，用直尺和

    圆规作出∠A的平分线与BC边交于点D（不写作法，保留作图痕迹）。

    在新图形中，你发现了什么？请写出两条。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点P1（a-1，5）和P2（2，b-1）关于x轴对称，则（a+b）2009的值为      

    查看答案和解析>>

    同步练习册答案