
【题目】如图,在平面直角坐标系中,直线l:y=x+1交x轴于点A,交y轴于点A1,A2,A3,…在直线l上,点B1,B2,B3…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn,顶点Bn的坐标为_____.

科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠BAC=90°,AB=AC,点P为AC上一点,M为BC上一点.
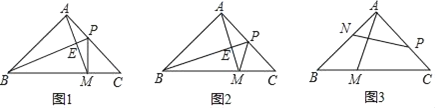
(1)若AM⊥BP于点E.
①如图1,BP为△ABC的角平分线,求证:PA=PM;
②如图2,BP为△ABC的中线,求证:BP=AM+MP.
(2)如图3,若点N在AB上,AN=CP,AM⊥PN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.
(1)求景点B与C的距离;
(2)为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
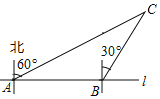
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
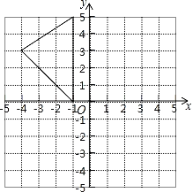
(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(情境)某课外兴趣小组在一次折纸活动课中.折叠一张带有条格的长方形的纸片ABCD(如图1),将点B分别与点A,A1,A2,…,D重合,然后用笔分别描出每条折痕与对应条格线所在的直线的交点,用平滑的曲线顺次连结各交点,得到一条曲线.
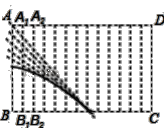
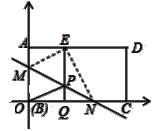
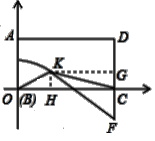
图1 图2 图3
(探索)(1)如图2,在平面直角坐标系xOy中,将矩形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB边放在y轴的正半轴上,AB=m,AD=n,(m≤n).将纸片折叠,使点B落在边AD上的点E处,过点E作EQ⊥BC于点Q,折痕MN所在直线与直线EQ相交于点P,连结OP.求证:四边形OMEP是菱形;
(归纳)(2)设点P坐标是(x,y),求y与x的函数关系式(用含m的代数式表示).
(运用)(3)将矩形纸片ABCD如图3放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在点K,使得△KCF的面积是△KOC面积的![]() ?若存在,写出点K的坐标;若不存在,请说明理由.
?若存在,写出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
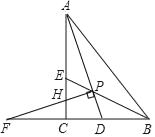
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
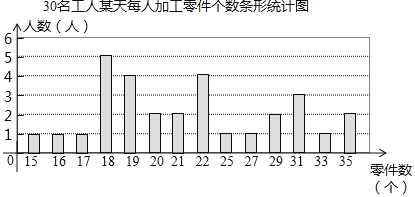
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com