
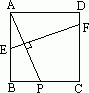
如图所示,已知正方形ABCD的边长为24cm,点P在BC上,且BP=10cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.
|
解:如图,过E作EG∥BC交CD于G.∴∠FGE=∠C=
∵四边形ABCD是正方形, ∴∠B=∠C= ∴四边形BCGE为矩形(三个角是直角的四边形是矩形). ∴EG=BC=AB(矩形对边相等). ∵∠AEG= ∴∠AEF+∠FEG=∠PAB+∠AEF= ∴∠PAB=∠FEG(同角的余角相等). ∴△ABP≌△EGF(ASA). ∴EF=AP(全等三角形对应边相等). ∴EF=AP= |
|
提示:为了求EF的长,需要把已知条件联系起来,因此想到构造一个以EF为边的直角三角形,所以作EG∥BC,则易证△ABP≌△EGF,从而根据勾股定理求值. |


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
 30、如图所示,已知正方形ABCD,E为BC上任意一点,延长AB至F,使BF=BE,AE的延长线交CF于G,
30、如图所示,已知正方形ABCD,E为BC上任意一点,延长AB至F,使BF=BE,AE的延长线交CF于G,查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( )
如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知正方形OABC的面积为9,点B在函数y=
如图所示,已知正方形OABC的面积为9,点B在函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com