
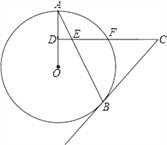
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;
(2)∠ABF的度数为30°;
(3)⊙O的半径为![]() .
.
【解析】试题分析:(1)连接OB,由圆的半径相等和已知条件证明∠OBC=90°,即可证明BC是 O的切线;(2)连接OF,AF,BF,首先证明△OAF是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数;(3)过点C作CG⊥BE于G,根据等腰三角形的性质得到EG=![]() BE=5,由两角相等的三角形相似,△ADE∽△CGE,利用相似三角形对应角相等得到sin∠ECG=sinA=
BE=5,由两角相等的三角形相似,△ADE∽△CGE,利用相似三角形对应角相等得到sin∠ECG=sinA=![]() ,在Rt△ECG中,利用勾股定理求出CG的长,根据三角形相似得到比例式,代入数据即可得到结果.
,在Rt△ECG中,利用勾股定理求出CG的长,根据三角形相似得到比例式,代入数据即可得到结果.
试题解析:(1)证明:连接OB
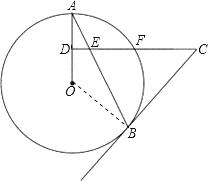
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC
又∵CD⊥OA
∴∠A+∠AED=∠A+∠CEB=90°
∴∠OBA+∠ABC=90°
∴OB⊥BC
∴BC是O的切线。
(2)连接OF,AF,BF,
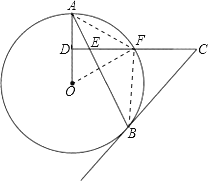
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°
∴∠ABF=![]() ∠AOF=30°
∠AOF=30°
(3)如图,过点C作CG⊥BE于G,
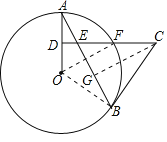
∵CE=CB,
∴EG=![]() BE=5,
BE=5,
∵∠ADE=∠CGE=90°,∠AED=∠GEC,
∴∠GCE=∠A,
∴△ADE∽△CGE,
∴sin∠ECG=sinA=![]() ,即CE=13,
,即CE=13,
在Rt△ECG中,
∵CG=![]() ,
,
∵CD=15,CE=13,
∴DE=2,
∵△ADE∽△CGE,
∴![]() ,
,
∴AD=![]() ,CG=
,CG=![]() ,
,
∴O的半径OA=2AD=![]() .
.


科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式x3﹣5xy2﹣7y3+8x2y按某一个字母的升幂排列,正确的是( )
A.x3﹣7y3﹣5xy2+8x2y
B.﹣7y3﹣5xy2+8x2y+x3
C.7y3﹣5xy2+8x2y+x3
D.x3﹣5xy2+8x2y﹣7y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安徽省2010年末森林面积为3804.2千公顷,用科学记数法表示3804.2千正确的是( )
A.3804.2×103B.380.42×104C.3.8042×106D.3.8042×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF. 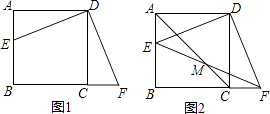
(1)如图1,求证:DF⊥DE;
(2)如图2,连接AC,EF交于点M,求证:M是EF的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com