
【题目】如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某—时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆乍的状况比第一辆好,他就上第二辆车;如果第二辆不比第—辆好,他就上第三辆车.若把这三辆车的舒适程度分为上、中、下三等.请问:
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
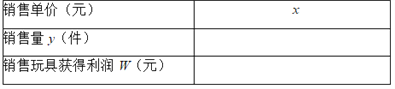
(2)在(1)条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A种品牌的文具比B种品牌的文具的单价少1元,小明买了2个A种品牌的文具和3个B种品牌的文具,一共花了28元,那么A种品牌的文具的单价是________元/个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.
(1)试探究BE与BF的数量关系,并证明你的结论;
(2)求EF的最大值与最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com