
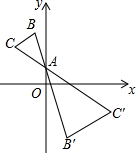
 如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )| A. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+3) | B. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-3) | C. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+2) | D. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-2) |
分析 过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,设C(x,y),则CD=y-2、AD=-x、C′D′=2-n、AD′=m,根据位似比为1:2得$\frac{CD}{C′D′}$=$\frac{AD}{AD′}$=$\frac{1}{2}$,即$\frac{y-2}{2-n}$=$\frac{-x}{m}$=$\frac{1}{2}$,计算即可.
解答 解:过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,
设C(x,y),
则CD=y-2、AD=-x,C′D′=2-n,AD′=m,
∵△ABC与△AB′C′的位似比为2:1,
∴$\frac{CD}{C′D′}$=$\frac{AD}{AD′}$=$\frac{1}{2}$,即$\frac{y-2}{2-n}$=$\frac{-x}{m}$=$\frac{1}{2}$,
解得:x=-$\frac{1}{2}$m,y=-$\frac{1}{2}$n+3,
∴点C的坐标为(-$\frac{1}{2}$m,-$\frac{1}{2}$n+3),
故选:A.
点评 本题考查的是位似变换的性质和坐标与图形的性质,掌握两个图形必须是相似形是解题的关键,注意相似三角形的性质的灵活运用.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$与-0.2 | B. | -$\frac{1}{3}$与0.333 | C. | -2.25与2$\frac{1}{4}$ | D. | 5与-(-5) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,4,5 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 32,42,52 | D. | 2,2,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | -3 | C. | -4 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com