
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
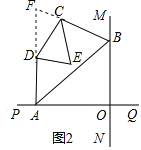
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
【答案】(1)∠AEB的大小不变135°;(2)∠CED的大小不变67.5°;(3)60°或45°.
【解析】
试题分析:(1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°,再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=![]() ∠OAB,∠ABE=
∠OAB,∠ABE=![]() ∠ABO,由三角形内角和定理即可得出结论;
∠ABO,由三角形内角和定理即可得出结论;
(2)延长AD、BC交于点F,根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°,进而得出∠OAB+∠OBA=90°,故∠PAB+∠MBA=270°,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知∠BAD=![]() ∠BAP,∠ABC=
∠BAP,∠ABC=![]() ∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;
∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;
(3))由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=![]() ∠BAO,∠EOQ=
∠BAO,∠EOQ=![]() ∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
解:(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=![]() ∠OAB,∠ABE=
∠OAB,∠ABE=![]() ∠ABO,
∠ABO,
∴∠BAE+∠ABE=![]() (∠OAB+∠ABO)=45°,
(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变.
延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=![]() ∠BAP,∠ABC=
∠BAP,∠ABC=![]() ∠ABM,
∠ABM,
∴∠BAD+∠ABC=![]() (∠PAB+∠ABM)=135°,
(∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=![]() ∠BAO,∠EOQ=
∠BAO,∠EOQ=![]() ∠BOQ,
∠BOQ,
∴∠E=∠EOQ﹣∠EAO=![]() (∠BOQ﹣∠BAO)=
(∠BOQ﹣∠BAO)=![]() ∠ABO,
∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°;
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°.
∴∠ABO为60°或45°.


科目:初中数学 来源: 题型:
【题目】直角坐标系中,点P(x,y)在第二象限,且P 到x 轴、y 轴距离分别为3,7,则P 点坐标为( )
A. (-3,7) B. (-7,3) C. (3,7) D. (7,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神农尝百草,泡泡青菜便是其中之一,小随同学利用假期开网店批发出售泡泡青菜,他打出促销广告:最优质泡泡青菜35箱,每箱售价30元,若一次性购买不超过10箱时,售价不变;若一次性购买超过10箱时,没多买1箱,所买的每箱泡泡青菜的售价均降低0.3元.已知该青菜成本是每箱20元,若不计其他费用,设顾客一次性购买泡泡青菜x(x为整数)箱时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少箱时,该网店从中获利最多,最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com