
 如图,在平面直角坐标系中,已知点A(2,3),点B(-2,1),在x轴上存在点P到A,B两点的距离之和最小,求P点的坐标.
如图,在平面直角坐标系中,已知点A(2,3),点B(-2,1),在x轴上存在点P到A,B两点的距离之和最小,求P点的坐标. 分析 作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,求出C的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出k、b,得出直线BC的解析式,求出直线与x轴的交点坐标即可.
解答 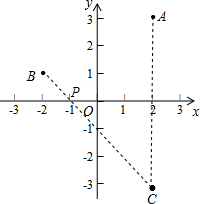 解:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
解:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
∵A点的坐标为(2,3),B点的坐标为(-2,1),
∴C(2,-3),
设直线BC的解析式是:y=kx+b,
把B、C的坐标代入得:
$\left\{\begin{array}{l}{-2k+b=1\\;}\\{2k+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
即直线BC的解析式是y=-x-1,
当y=0时,-x-1=0,
解得x=-1,
∴P点的坐标是(-1,0).
点评 本题考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,轴对称-最短路线问题的应用,解题的关键是根据两点之间线段最短,找出P点的位置.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 161,18 | B. | 162,17 | C. | 162,18 | D. | 161,17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?画树状图或列表说明理由.
用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?画树状图或列表说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
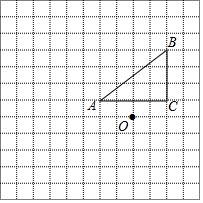 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com