练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某商场购进一批单价为4元的日用品．若按每件5元的价格销售，每月能卖出3万件；若按每件6元的价格销售，每月能卖出2万件，假定每月销售件数y（件）与价格x（元/件）之间满足一次函数关系．
    （1）试求y与x之间的函数关系式；
    （2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？

    【答案】
    （1）解：由题意，可设y=kx+b（k≠0），

    把（5，30000），（6，20000）代入得： ，

    解得： ，

    所以y与x之间的关系式为：y=﹣10000x+80000；


    （2）解：设利润为W元，则W=（x﹣4）（﹣10000x+80000）

    =﹣10000（x﹣4）（x﹣8）

    =﹣10000（x2﹣12x+32）

    =﹣10000[（x﹣6）2﹣4]

    =﹣10000（x﹣6）2+40000

    所以当x=6时，W取得最大值，最大值为40000元．

    答：当销售价格定为6元时，每月的利润最大，每月的最大利润为40000元．


    【解析】（1）利用待定系数法求得y与x之间的一次函数关系式；（2）根据“利润=（售价﹣成本）×售出件数”，可得利润W与销售价格x之间的二次函数关系式，然后求出其最大值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】根据图中给出的信息，解答下列问题：

    （1）放入一个小球水面升高 ，，放入一个大球水面升高 ；

    （2）如果要使水面上升到50，应放入大球、小球各多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是边长分别为4 和2的两个等边三角形纸片ABC和OD′E′叠放在一起（C与O重合）．
    （1）操作：固定△ABC，将△ODE绕点C顺时针旋转30°，后得到△ODE，连接AD、BE、CE的延长线交AB于F（图2）： 探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
    （2）在（1）的条件下将△ODE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR，当点P与点F重合时停止运动（图3）． 探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
    （3）将图1中△ODE固定，把△ABC沿着OE方向平移，使顶点C落在OE的中点G处，设为△ABG，然后奖△ABG绕点G顺时针旋转，边BG交边DE于点M，边AG交边DO于点N，设∠BGE=α（30°＜α＜90°）（图4）． 探究：在图4中，线段ONEM的值是否随α的变化而变化？如果没有变化，请你求出ONEM的值，如果有变化，请你说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形OABC的顶点A、C的坐标分别是（4，0）和（0，2），反比例函数y= （x＞0）的图象过对角线的交点P并且与AB，BC分别交于D，E两点，连接OD，OE，DE，则△ODE的面积为 ．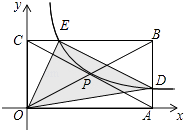

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

    （2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等腰△ABC中，AD垂直于直线BC，垂足为点D，且AD＝BC，则△ABC底角的度数为(　　)

    A. 45° B. 75° C. 45°或75°或15° D. 60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．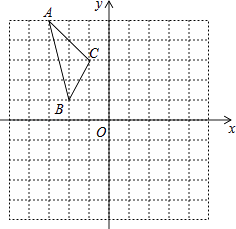

    （1）若△ABC经过平移后得到△A1B1C1 ， 已知点C1的坐标为（4，0），写出顶点A1 ， B1的坐标；
    （2）若△ABC和△A2B2C2关于原点O成中心对称图形，写出△A2B2C2的各顶点的坐标；
    （3）将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 ， 写出△A3B3C3的各顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2016年9月5日，二十国集团领导人杭州峰会在杭州国际博览中心继续举行，这次峰会吸引了大批游客在“十一”假期间前往杭州旅游．为抓住商机，两个商家对同样一件售价为50元/个的产品进行促销活动．甲商家用如下方法促销：若购买该商品不超过l0个，按原价付款：若一次购买l0个以上．且购买的个数每增加一个，其价格减少l元，但该商品的售价不得低于35元/个；乙店一律按原价的80%销售．现购买该商品x个，如果全部在甲商家购买，则所需金额为y1元：如果全部在乙商家购买，则所需金额为y2元．
    （1）分别求出yl ， y2与x之间的函数关系式；
    （2）若一位游客花800元，最多能购买多少个该商品？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，点A的坐标为（﹣2，0），OB=OA，且∠AOB=120°．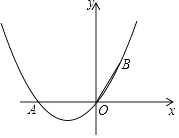

    （1）求经过A，O，B三点的抛物线的解析式．
    （2）在（1）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由．
    （3）若点M为抛物线上一点，点N为对称轴上一点，是否存在点M，N使得A，O，M，N构成的四边形是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案