
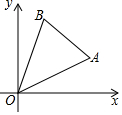
 如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b)
如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b)分析 (1)利用二次根式的混合运算法则,求出c即可;
(2)①如图1中,作BE⊥y轴于E,AF⊥x轴于F,EB的延长线交FA的延长线于M.首先证明四边形OEMF是正方形,将△OEB绕点O顺时针旋转90°得到△OFG,只要证明△OAB≌△OAG,即可推出AB=AG,由AG=AF+FG=AF+BE,推出AB=BE+AF=2a-3b+b=2a-2b;
②由OF=OE=a,AF=b,a-b=2$\sqrt{3}$-2,推出OF=FM=a=2$\sqrt{3}$-2+b=AF+AM,推出AM=2$\sqrt{3}$-2,AB=2(a-b)=4$\sqrt{3}$-4,在Rt△ABM中,BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=$\sqrt{(4\sqrt{3}-4)^{2}-(2\sqrt{3}-2)^{2}}$=6-2$\sqrt{3}$,由EM=FM,可知EB+EM=AM+AF,推出4$\sqrt{3}$-4-b+6-2$\sqrt{3}$=2$\sqrt{3}$-2+b,推出b=2,由此即可解决问题.
解答 解:(1)∵c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$,a>0,b>0,
∴C=$\sqrt{4{a}^{2}}$-$\sqrt{9{b}^{2}}$=2a-3b,
∴B(2a-3b,a).
(2)①如图1中,作BE⊥y轴于E,AF⊥x轴于F,EB的延长线交FA的延长线于M.
∵∠MEO=∠MFO=∠EOF=90°,
∴四边形OEMF是矩形,
∵B(2a-3b,a),A(a,b),
∴OE=OF=a,
∴四边形OEMF是正方形,将△OEB绕点O顺时针旋转90°得到△OFG,
∵∠AOB=45°,
∴∠EOB+∠AOF=45°,
∴∠AOG=∠AOF+∠FOG=45°,
∴∠AOB=∠AOG=45°,∵OA=OA,OB=OG,
∴△OAB≌△OAG,
∴AB=AG,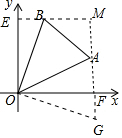
∵AG=AF+FG=AF+BE,
∴AB=BE+AF=2a-3b+b=2a-2b.
②∵OF=OE=a,AF=b,a-b=2$\sqrt{3}$-2,
∴OF=FM=a=2$\sqrt{3}$-2+b=AF+AM,
∴AM=2$\sqrt{3}$-2,AB=2(a-b)=4$\sqrt{3}$-4,
在Rt△ABM中,BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=$\sqrt{(4\sqrt{3}-4)^{2}-(2\sqrt{3}-2)^{2}}$=6-2$\sqrt{3}$,
∵EM=FM,
∴EB+EM=AM+AF,
∴4$\sqrt{3}$-4-b+6-2$\sqrt{3}$=2$\sqrt{3}$-2+b,
∴b=2,
∴OF=2$\sqrt{3}$-2+2=2$\sqrt{3}$,
∴A(2$\sqrt{3}$,2).
点评 本题考查三角形综合题、正方形的判定和性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题,学会利用参数构建方程,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
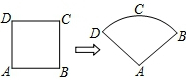 如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB的度数是$\frac{360}{π}$度.(结果保留π)
如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB的度数是$\frac{360}{π}$度.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
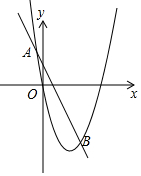 如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,
如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
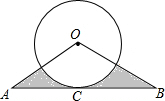 如图,在△ABC中,OA=OB=6,∠O=120°,以点O为圆心的⊙O和底边AB相切于点C,则阴影部分的面积为9$\sqrt{3}$-3π..
如图,在△ABC中,OA=OB=6,∠O=120°,以点O为圆心的⊙O和底边AB相切于点C,则阴影部分的面积为9$\sqrt{3}$-3π..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 18 | 27 |
| d(x) | 3a-b+c | 2a+b | a-c | 1+a+b+c | 3-3a+3c | 4a+2b | 3-b-2c | 6a+3b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com