
 如图,在四边形ABCD中,对角线AC⊥BD且AC=6,BD=8,点E、F、G分别是边AB、CD、AD的中点,则EF=5.
如图,在四边形ABCD中,对角线AC⊥BD且AC=6,BD=8,点E、F、G分别是边AB、CD、AD的中点,则EF=5. 分析 先利用三角形中位线性质得到EG=$\frac{1}{2}$BD=4,EG∥BD,GF=$\frac{1}{2}$AC=3,GF∥AC,再判断EG⊥GF,然后利用勾股定理计算EF的长.
解答 解:∵点E、F、G分别是边AB、CD、AD的中点,
∴EG为△ABC的中位线,GF为△DAC的中位线,
∴EG=$\frac{1}{2}$BD=4,EG∥BD,GF=$\frac{1}{2}$AC=3,GF∥AC,
∵AC⊥BD,
∴EG⊥GF,
在Rt△GEF中,EF=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为5.
点评 本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | 2-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
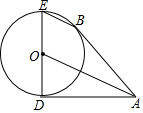 如图,AB,AD为⊙O的切线,切点分别为B,D,DE为⊙O的直径,连接BE,OA
如图,AB,AD为⊙O的切线,切点分别为B,D,DE为⊙O的直径,连接BE,OA查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
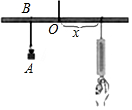 如图所示,小华设计了一个研究杠杆平衡条件的实验,在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A,在中点的右侧用一个弹簧秤向下拉,改变弹簧与点O的距离x(cm)观察弹簧的示数y(N)的变化情况,实验数据记录如下:
如图所示,小华设计了一个研究杠杆平衡条件的实验,在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A,在中点的右侧用一个弹簧秤向下拉,改变弹簧与点O的距离x(cm)观察弹簧的示数y(N)的变化情况,实验数据记录如下:| x(cm) | … | 10 | 15 | 20 | 25 | 30 | … |
| y(N) | … | 30 | 20 | 15 | 12 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件“任意一个x(x为实数)值,x2是不确定事件” | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投十次一定投中6次 | |
| C. | 为了了解我市各超市销售的速冻食品质量情况,适合采取普查的方式调查 | |
| D. | 投掷一枚质地均匀的硬币10次,可能有5次正面向上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com