练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
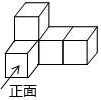
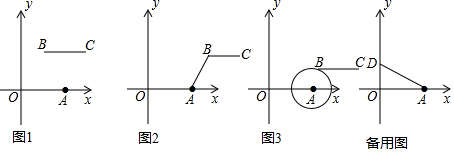
    19．如图，简单几何体的左视图是（　　）
    A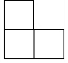．B．C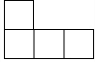．D．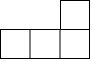

    分析 根据从左边看得到的图形是左视图，可得答案．

    解答 解：从左边看第一层是两个小正方形，第二层左边一个小正方形，
    故选：A．

    点评 本题考查了简单组合体的三视图，从左边看得到的图形是左视图．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．如图，某教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2m的影子CE；而当光线与地面夹角是45°时，教学楼顶部A在地面上的影子F与墙角C的距离为18m（B、F、C在同一直线上）．求教学楼AB的高；（结果保留整数）（参考数据：sim22°≈0.37，cos22°≈0.93，tan22°≈0.40）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

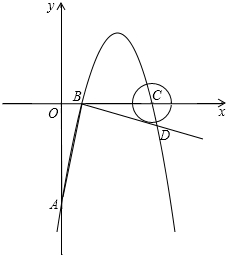    10．如图，在平面直角坐标系中，抛物线y=ax2+6x+c（a≠0）交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，-5），点B的坐标为（1，0）．
    （1）求此抛物线的解析式及定点坐标；
    （2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C的位置关系，并说明理由；
    （3）在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，抛物线y=ax2+bx+c与x轴交于A（1，0），B（3，0）两点，与y轴交于点C（0，3）．
    （1）求抛物线的解析式；
    （2）若点M是x轴下方的抛物线上的一个动点，过点M作MN⊥x轴，交直线BC于点N，求四边形MBNA的最大面积，并求出点M的坐标；
    （3）在抛物线上是否存在一点P，使△BCP为直角三角形？若存在，求出P点坐标，如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．小明在投篮训练中作了大量的统计，得到自己投中的概率为0.6，则小明在一次训练中投了50次，他投中的次数在30次左右．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列运算中，正确的是（　　）
    A．（x+1）2=x2+1B．（x2）3=x5C．2x4•3x2=6x8D．x2÷x-1=x3（x≠0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．定义：P、Q分别是两条线段a，b上任意一点，线段PQ长度的最小值叫做线段a与线段b的距离．已知，O（0，0），A（4，0），B（m，n），C（m+4，n）是平面直角坐标系中四点．
    （1）根据上述定义，当m=2，n=2时，如图1，线段BC与线段OA的距离为2；当m=5，n=2时，如图2，线段BC与线段OA的距离（即线段AB的长）为$\sqrt{5}$；
    （2）如图3，若点B落在圆心为A，半径为2的圆上，线段BC与线段OA的距离记为d，求d关于m的函数解析式．
    （3）当m值变化时，动线段BC与线段OA的距离始终为2，线段BC的中点为M，点D（0，2），m≥0，n≥0，作MH⊥x轴，垂足为H，是否存在m值，使以A、M、H为顶点的三角形与△AOD相似？若存在，求出m值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．估计$\sqrt{38}$的值在（　　）
    A．4和5之间B．5和6之间C．6和7之间D．7和8之间

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如表为初三（1）班全部43名同学某次数学测验成绩的统计结果，则下列说法正确的是（　　）
     成绩（分） 70 80 90
     男生（人） 5 10 7
     女生（人） 4 13 4
    A．男生的平均成绩大于女生的平均成绩
    B．男生的平均成绩小于女生的平均成绩
    C．男生成绩的中位数大于女生成绩的中位数
    D．男生成绩的中位数小于女生成绩的中位数

    查看答案和解析>>

    同步练习册答案