
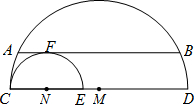
 如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设
如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设 |
| CD |
 |
| CE |
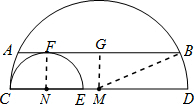 解:过M作MG⊥AB于G,连MB,NF,如图,
解:过M作MG⊥AB于G,连MB,NF,如图,

科目:初中数学 来源: 题型:
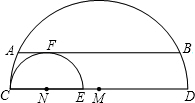 如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=10,设弧CD、弧CE的长分别为x、y,线段ED的长为z,则z(x+y)的值为
如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=10,设弧CD、弧CE的长分别为x、y,线段ED的长为z,则z(x+y)的值为查看答案和解析>>
科目:初中数学 来源:2012届安徽马鞍山含山一中九年级第二学期数学月考试卷(带解析) 题型:解答题
如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设 、
、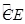 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
查看答案和解析>>
科目:初中数学 来源:2011-2012学年安徽马鞍山含山一中九年级第二学期数学月考试卷(解析版) 题型:解答题
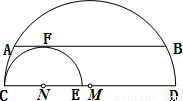
如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设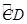 、
、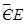 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
查看答案和解析>>
科目:初中数学 来源:2012届度临沂市费县八年级第二学期期末检测数学 题型:填空题
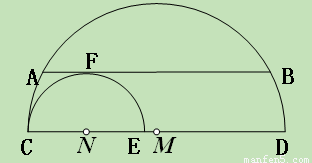
(11·孝感)如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设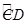 、
、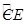 的长分别为
的长分别为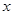 、
、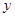 ,线段ED的长为
,线段ED的长为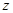 ,则
,则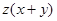 的值为____________.
的值为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com