
分析 (1)利用一元二次方程根的判别式证明;
(2)根据题意求出m的值,解一元二次方程即可.
解答 (1)证明:2x2-mx-m2=0,
△=(-m)2-4×2×(-m2)
=m2+8m2
=9m2≥0,
∴对于任意实数m,二次函数y=2x2-mx-m2的图象与x轴总有公共点;
(2)解:由题意得,2×12-m-m2=0,
整理得,m2+m-2=0,
解得,m1=1,m2=-2,
当m=1时,二次函数为y=2x2-x-1,
当y=0时,2x2-x-1=0,
解得,x1=1,x2=-$\frac{1}{2}$,
则点A的坐标为(-$\frac{1}{2}$,0),
当m=-2时,二次函数为y=2x2+2x-4,
当y=0时,2x2-x-1=0,
解得,x1=1,x2=-2,
则点A的坐标为(-2,0),
终上所述,A点坐标为(-$\frac{1}{2}$,0)或(-2,0).
点评 本题考查的是抛物线与x轴的交点问题,掌握二次函数与一元二次方程的关系、正确解出一元二次方程是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
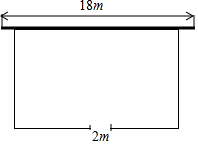 如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在方格纸中,每个小正方形的边长均为1,△ABC的顶点A、B、C均在小正方形的顶点上.
如图,在方格纸中,每个小正方形的边长均为1,△ABC的顶点A、B、C均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
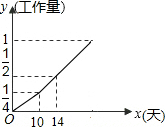 甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入合作,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系.
甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入合作,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com