
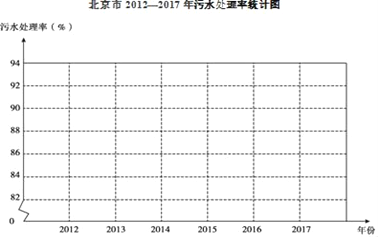
【题目】北京市积极开展城市环境建设,其中污水治理是重点工作之一,以下是北京市2012﹣2017年污水处理率统计表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
污水处理率(%) | 83.0 | 84.6 | 86.1 | 87.9 | 90.0 | 92.0 |
(1)用折线图将2012﹣2017年北京市污水处理率表示出来,并在图中标明相应的数据;
(2)根据统计图表中提供的信息,预估2018年北京市污水处理率约为_____%,说明你的预估理由:_____.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
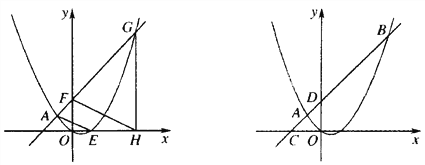
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求![]() 之值(用含m的代数式表示);
之值(用含m的代数式表示);
(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒![]() 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
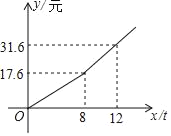
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水8吨以内(包括8吨)和用水8吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
(1)求出自来水公司在这两个用水范围内的收费标准;
(2)若芳芳家6月份共交水费28.1元,请写出用水量超过8吨时应交水费y(元)与用水量x(吨)之间的函数关系,并求出芳芳家6月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
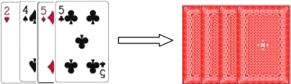
【题目】如图,甲、乙用这4张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上.
(1)甲从中任抽取一张,抽到4的概率是多少?
(2)甲、乙没人抽一张,甲先抽,乙后抽,抽出的牌不放回,甲、乙约定;只有甲抽到的牌面数字比乙大时甲胜.请你用树状图或列表法说明甲、乙获胜的机会是否相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形OABC的顶点O、A、C的坐标分别为O(0,0),A(﹣x,0),C(0,y),且x、y满足![]() .
.
(1)矩形的顶点B的坐标是 .
(2)若D是AB中点,沿DO折叠矩形OABC,使A点落在点E处,折痕为DO,连BE并延长BE交y轴于Q点.
①求证:四边形DBOQ是平行四边形.
②求△OEQ面积.
(3)如图2,在(2)的条件下,若R在线段AB上,AR=4,P是AB左侧一动点,且∠RPA=135°,求QP的最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
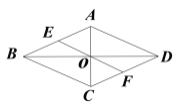
【题目】如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是( )
(1)t=5时,s=150;(2)t=35时,s=450;(3)甲的速度是30米/分;(4)t=12.5时,s=0.

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
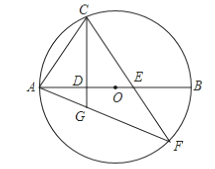
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB于点D,E是AB上一点,直线CE与⊙O交于点F,连结AF,与直线CD交于点G.
求证:(1)∠ACD=∠F; (2)AC2=AG·AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在平面直角坐标系中,A(﹣3,﹣4),B(0,﹣2).
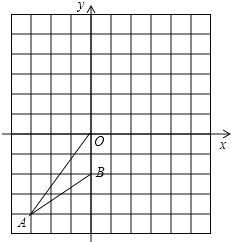
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标;
(2)判断以A,B,A1,B1为顶点的四边形的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com