
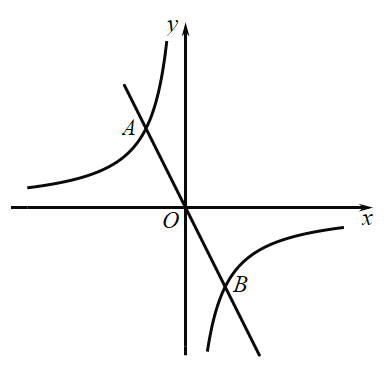
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式及点![]() 的坐标;
的坐标;
(2)点![]() 是第四象限内反比例函数图象上一点,过点
是第四象限内反比例函数图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
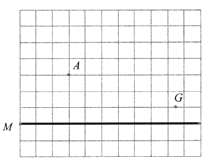
【题目】如图,在每个小正方形的边长为1的网格中,A,M,N均在格点上.在线段![]() 上有一动点B,以
上有一动点B,以![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,使
,使![]() ,
,![]() ,G是一个小正方形边的中点.
,G是一个小正方形边的中点.
(1)当点B的位置满足![]() 时,求此时
时,求此时![]() 的长_______;
的长_______;
(2)请用无刻度的直尺,在如图所示的网格中,画出一个点C,使其满足线段![]() 最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: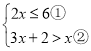 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(1)解不等式①,得: ;
(2)解不等式②得: ;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
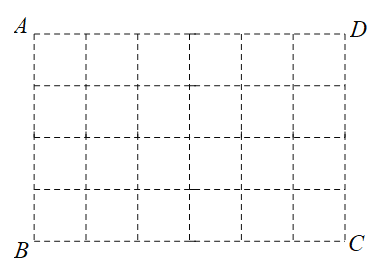
【题目】如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.
(1)在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH;
(2)在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
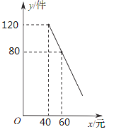
【题目】某商店购进一批成本为每件40元的商品,经调查发现,该商品每天的销售量![]() (件
(件![]() 与销售单价
与销售单价![]() (元
(元![]() 之间满足一次函数关系,其图象如图所示.
之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(2)若商店要使销售该商品每天获得的利润等于1000元,每天的销售量应为多少件?
(3)若商店按单价不低于成本价,且不高于65元销售,则销售单价定为多少元时,才能使销售该商品每天获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
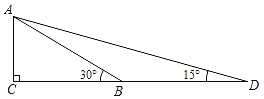
【题目】构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°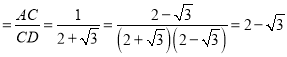 .类比这种方法,计算tan22.5°的值为( )
.类比这种方法,计算tan22.5°的值为( )
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C
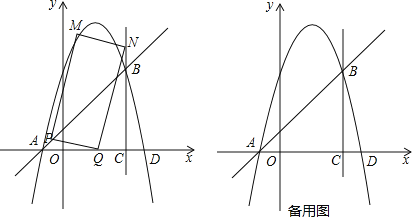
(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
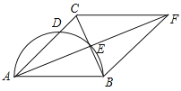
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB、FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圆的面积.
,BE=1,求半圆的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com