
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
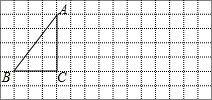 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
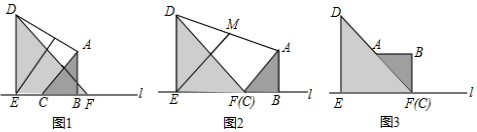
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
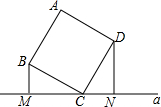 如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N
如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)
有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com