
【题目】如图,AB∥CD,直线EF分别与AB,CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°. 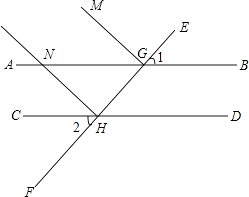
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)∠HNG=°.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和为 . 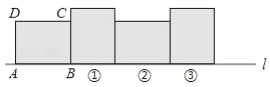
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= ![]() BC,连接CD和EF.
BC,连接CD和EF. 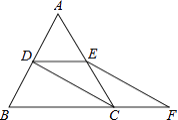
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为完成下列任务,你认为采用什么调查方式最合适?
(1)了解某市居民的年人均收入;
(2)了解某班学生期末考试的数学成绩;
(3)了解一个月内某城市一条道路的车流量;
(4)了解某电视台一个娱乐节目的收视率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com