已知:抛物线y=-x2+(k+1)x+2k+1经过点A(0,3).
(1)求k的值;
(2)设抛物线交x轴于B、C两点(B在C右边),点P(m,n)是抛物线上的一个动点,且位于直线AB上方,设△PAB的面积为s,试写出s关于x的函数关系式,并求出s的最大值;
(3)平行于x轴的一条直线交抛物线于E、F两点,若以EF为直径的圆恰好与x轴相切,求此圆的半径.
分析:(1)将A点坐标代入抛物线解析式,可求k的值;
(2)求出抛物线与直线AB的解析式,用m表示P、E两点的纵坐标,得出PE长的表达式,由s=
×PE×OB求△PAB面积的表达式,利用二次函数的性质求最大值;
(3)设圆的半径为r,分为EF在x轴上方时,EF在x轴下方时,两种情况,由抛物线与圆的对称性,圆心在抛物线对称性x=1上,可知点F的坐标为(r+1,r)或(r+1,-r),分别代入抛物线解析式可求r的值.
解答: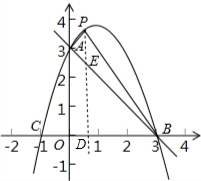
解:(1)∵抛物线经过点A(0,3),
∴2k+1=3,
∴k=1;(3分)
(2)作PD⊥x轴于点D,交直线AB于E点,
∵k=1时,抛物线解析式为y=-x
2+2x+3,则A(0,3),B(3,0),
∴直线AC解析式为y=-x+3,
∵点P(m,n)在抛物线上,
∴n=-m
2+2m+3,PE=(-m
2+2m+3)-(-m+3)=-m
2+3m,
∴s=
×PE×OB=
(-m
2+3m)=-
(m-
)
2+
,
∴当m=
时,s取最大值为
;(7分)
(3)设圆的半径为r.
①当EF在x轴上方时,
由抛物线及直线与圆相切的性质可得:点F的坐标为(r+1,r)
代入y=-x
2+2x+3得:-(r+1)
2+2(r+1)+3=r,
即r
2+r-4=0
解得:
r=(r取正数)(10分)
②当EF在x轴下方时,
由抛物线及直线与圆相切的性质可得:点F的坐标为(r+1,-r),
代入y=-x
2+2x+3得:-(r+1)
2+2(r+1)+3=-r,
即r
2-r-4=0,
解得:
r=(r取正数)
由①②知:
r=或
r=.(13分)
点评:本题考查了二次函数的综合运用.关键是根据抛物线解析式,形数结合,表示三角形面积,根据圆与抛物线的轴对称性,确定圆与x轴相切时,F点的坐标.

 解:(1)∵抛物线经过点A(0,3),
解:(1)∵抛物线经过点A(0,3),

 阅读快车系列答案
阅读快车系列答案