
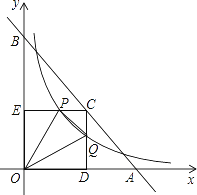
【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线y=![]() 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且![]() ,则k的值是( )
,则k的值是( )
A. 4 B. 2 C. ![]() D.
D. ![]()
【答案】B
【解析】四边形ODCE为正方形,则OC是第一象限的角平分线,则解析式是y=x,即可求得C的坐标,根据反比例函数一定关于y=x对称,则P、Q一定是对称点,则设Q的坐标是(2,a),则DQ=EP=a,PC=CQ=2﹣a,根据正方形ODCE的面积﹣△ODQ的面积﹣△OEP的面积﹣△PCQ的面积=△OPQ的面积,即可列方程求得a的值,求得Q的坐标,利用待定系数法即可求得k的值.
四边形ODCE为正方形,则OC是第一象限的角平分线,则解析式是y=x,
根据题意得: ![]() ,
,
解得: ![]() ,
,
则C的坐标是(2,2),
设Q的坐标是(2,a),
则DQ=EP=a,PC=CQ=2﹣a,
正方形ODCE的面积是:4,
S△ODQ=![]() ×2a=a,同理S△OPE=a,S△CPQ=
×2a=a,同理S△OPE=a,S△CPQ= ![]() (2﹣a)2 ,
(2﹣a)2 ,
则4﹣a﹣a﹣ ![]() (2﹣a)2=
(2﹣a)2= ![]() ,
,
解得:a=1或﹣1(舍去),
则Q的坐标是(2,1),
把(2,1)代入![]() 得:k=2.
得:k=2.
故选B.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
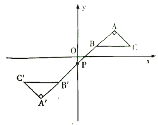
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 关于点
关于点![]() 成中心对称,则点
成中心对称,则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.同物几何?
即:一个整数除以3余2,除以5余3,除以7余2,则这个整数为__________________.(写出符合题意且不超过300的3个正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
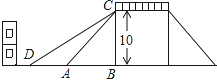
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
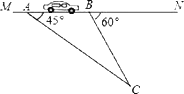
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示
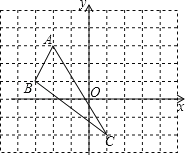
(1)请画出△ABC关于y轴对称的△A′B′C′;(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′B′C′三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com