
分析 (1)设甲用户该月用水x吨,乙用户该月用水y吨,根据总费用=单价×用水数量结合乙用户交水费31.5元(甲用户比乙用户多交水费37.5元),即可得出关于y(x)的一元一次方程,解之即可得出结论;
(2)根据应交水费=10×4.5+(20-10)×8+(用水量-20)×10,即可得出结论.
解答 解:(1)设甲用户该月用水x吨,乙用户该月用水y吨,
根据题意得:4.5y=31.5,4.5×10+8(y-10)=37.5+31.5,
解得:y=7,x=13.
答:甲用户该月用水13吨,乙用户该月用水7吨.
(2)4.5×10+8×(20-10)+10×(25-20)=175(元).
答:用25吨水应交175元水费.
点评 本题考查了一元一次方程的应用,解题的关键是:(1)根据总费用=单价×用水数量,列出关于y(x)的一元一次方程;(2)根据数量关系,列式计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
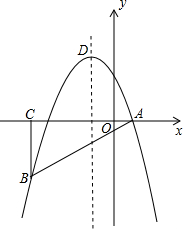 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.
如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成了扇形统计图.
小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成了扇形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在边长为1的小正方形网格中,△AOB的顶点均在格上,且坐标分别为A(1,2),B(3,1),O(0,0)
在边长为1的小正方形网格中,△AOB的顶点均在格上,且坐标分别为A(1,2),B(3,1),O(0,0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
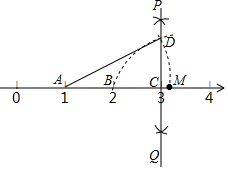 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{5}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com