
【题目】如图所示,初三数学兴趣小组同学为了测量垂直于水平地面的一座大厦AB的高度,一测量人员在大厦附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了60米后到达D处,在D处测得A处的仰角大小为30°,则大厦AB的高度约为多少米?(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有 ;
②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形 “十字形”.(填“是”或“不是”)
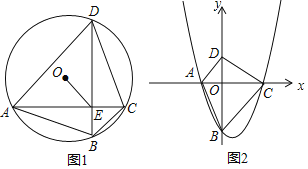
(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;
(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;
①![]() =
=![]()
![]() ;②
;②![]()
![]() =
=![]()
![]() ;③“十字形”ABCD的周长为12
;③“十字形”ABCD的周长为12![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
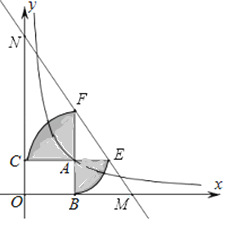
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
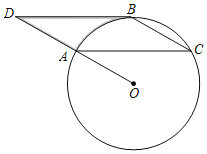
【题目】如图,点A、B、C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°.
(1)求证:BD是⊙O的切线;
(2)图中线段AD、BD和![]() 围成的阴影部分的面积= .
围成的阴影部分的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
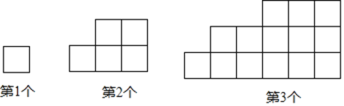
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3AB=3![]() ,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=______.
,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
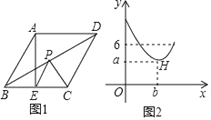
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
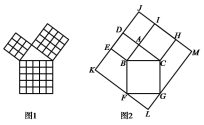
【题目】在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,![]() ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com