
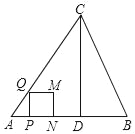
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC=5£¬AB±ßÉĻµÄøßCD=4£¬µćP“ÓµćA³ö·¢£¬ŃŲABŅŌĆæĆė3øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµćBŌĖ¶Æ£¬µ±µćP²»ÓėµćA”¢BÖŲŗĻŹ±£¬¹żµćP×÷PQ”ĶAB£¬½»±ßAC»ņ±ßBCÓŚµćQ£¬ŅŌPQĪŖ±ßĻņÓŅ²ą×÷Õż·½ŠĪPQMN£®ÉčÕż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖĶ¼ŠĪµÄĆ껿ĪŖS£ØĘ½·½µ„Ī»£©£¬µćPŌĖ¶ÆµÄŹ±¼äĪŖt£ØĆė£©£®
£Ø1£©Ö±½ÓŠ“³ötanBµÄÖµĪŖ”” ””£®
£Ø2£©ĒóµćMĀäŌŚ±ßBCÉĻŹ±tµÄÖµ£®
£Ø3£©µ±Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖĪŖĖıߊĪŹ±£¬ĒóSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø4£©±ßBC½«Õż·½ŠĪPQMNµÄĆ껿·ÖĪŖ1£ŗ3Į½²æ·ÖŹ±£¬Ö±½ÓŠ“³ötµÄÖµ£®
”¾“š°ø”æ£Ø1£©2£» £Ø2£©![]() £»£Ø3£©s=
£»£Ø3£©s=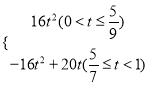 .£Ø4£©
.£Ø4£©![]() s£®
s£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĄūÓĆČż½ĒŗÆŹż¶ØŅåĒótanBµÄÖµ.(2) µ±µćMĀäŌŚBC±ßÉĻŹ±£¬ÓÉĢāŅāµĆ£ŗAP=3t£¬ĄūÓĆtan”ĻCAB=![]() ĒótµÄÖµ.(3) ¢Łµ±0£¼t”Ü
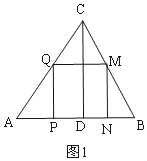
ĒótµÄÖµ.(3) ¢Łµ±0£¼t”Ü![]() Ź±£¬ČēĶ¼1£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒÕż·½ŠĪPQMN£¬¢Śµ±NÓėBÖŲŗĻŹ±,µ±
Ź±£¬ČēĶ¼1£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒÕż·½ŠĪPQMN£¬¢Śµ±NÓėBÖŲŗĻŹ±,µ±![]() £¼t£¼
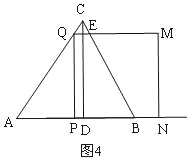
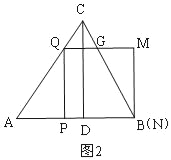
£¼t£¼![]() Ź±£¬ČēĶ¼3£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĪå±ßŠĪEQPNF£¬¢Ūµ±
Ź±£¬ČēĶ¼3£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĪå±ßŠĪEQPNF£¬¢Ūµ±![]() ”Üt£¼1Ź±£¬ČēĶ¼4£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĢŻŠĪEQPB£¬SÓėtÖ®¼äµÄŗÆŹż.(4) QG=GM£¬ t=
”Üt£¼1Ź±£¬ČēĶ¼4£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĢŻŠĪEQPB£¬SÓėtÖ®¼äµÄŗÆŹż.(4) QG=GM£¬ t=![]() s»ņ1sŹ±£¬±ßBC½«Õż·½ŠĪPQMNµÄĆ껿·ÖĪŖ1£ŗ3Į½²æ·Ö£®
s»ņ1sŹ±£¬±ßBC½«Õż·½ŠĪPQMNµÄĆ껿·ÖĪŖ1£ŗ3Į½²æ·Ö£®
ŹŌĢā½āĪö£ŗ
½ā£ŗ£Ø1£©”ßCD”ĶAB£¬
”ą”ĻADC=”ĻADB=90”ć£¬
”ßŌŚRt”÷ACDÖŠ£¬AD=![]() =3£¬
=3£¬
”ąBD=AB©AD=5©3=2£¬
”ąŌŚRt”÷BCDÖŠ£¬tan”ĻB=![]() =
=![]() =2£»
=2£»
¹Ź“š°øĪŖ2£®
£Ø2£©µ±µćMĀäŌŚBC±ßÉĻŹ±£¬ČēĶ¼1£¬
ÓÉĢāŅāµĆ£ŗAP=3t£¬
tan”ĻCAB=![]() £¬
£¬
”ąPQ=PN=MN=4t£¬BN=2t£¬
”ą3t+4t+2t=5£¬
t=![]() .
.
£Ø3£©·ÖČżÖÖĒéæö£ŗ
¢Łµ±0£¼t”Ü![]() Ź±£¬ČēĶ¼1£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒÕż·½ŠĪPQMN£¬
Ź±£¬ČēĶ¼1£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒÕż·½ŠĪPQMN£¬
”ąS=PQ2=£Ø4t£©2=16t2£»
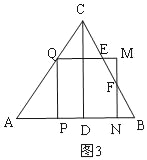
¢Śµ±NÓėBÖŲŗĻŹ±£¬ČēĶ¼2£¬
AP=3t£¬PQ=PB=4t£¬
”ą3t+4t=5£¬
t=![]() ,
,
µ±![]() £¼t£¼
£¼t£¼![]() Ź±£¬ČēĶ¼3£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĪå±ßŠĪEQPNF£¬
Ź±£¬ČēĶ¼3£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĪå±ßŠĪEQPNF£¬
¢Ūµ±![]() ”Üt£¼1Ź±£¬ČēĶ¼4£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĢŻŠĪEQPB£¬
”Üt£¼1Ź±£¬ČēĶ¼4£¬Õż·½ŠĪPQMNÓė”÷ABCÖŲµž²æ·ÖŹĒĢŻŠĪEQPB£¬
”ąAP=3t£¬PN=4t£¬
”ąBN=7t©5£¬PB=4t©£Ø7t©5£©=©3t+5£¬
ŌŚRt”÷APQÖŠ£¬AQ=5t£¬
”ąQC=5©5t£¬
”ßAC=AB£¬
”ą”ĻACB=”ĻABC£¬
”ßQE”ĪAB£¬
”ą”ĻQEC=”ĻABC£¬
”ą”ĻQEC=”ĻACB£¬
”ąQE=QC=5©5t£¬
”ąS=SĢŻŠĪQPBE=![]() £ØQE+PB£©”ĮPQ£¬
£ØQE+PB£©”ĮPQ£¬
=![]() £Ø5©5t+5©3t£©”Į4t=©16t2+20t£»
£Ø5©5t+5©3t£©”Į4t=©16t2+20t£»
×ŪÉĻĖłŹö£¬SÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
S=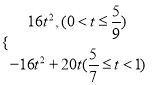 .
.
£Ø4£©ČēĶ¼2£¬µ±t=![]() Ź±£¬CQ=QG=5©5t=
Ź±£¬CQ=QG=5©5t=![]() £¬
£¬
”ąGM=4t©![]() =
=![]() £¬
£¬
”ąQG=GM£¬
”ąS”÷QGB=S”÷GMB£¬
”ąSĢŻŠĪGQPB£ŗS”÷GMB=3£ŗ1£¬
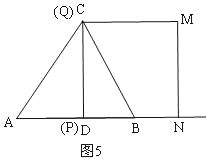
µ±PÓėDÖŲŗĻŹ±£¬t=1£¬ČēĶ¼5£¬
ŌņS”÷CDB£ŗSĖıߊĪCBNM=![]() ”Į2”Į4£ŗ£Ø42©
”Į2”Į4£ŗ£Ø42©![]() ”Į2”Į4£©£¬
”Į2”Į4£©£¬
=1£ŗ3£¬
×ŪÉĻĖłŹö£¬t=![]() s»ņ1sŹ±£¬±ßBC½«Õż·½ŠĪPQMNµÄĆ껿·ÖĪŖ1£ŗ3Į½²æ·Ö£®
s»ņ1sŹ±£¬±ßBC½«Õż·½ŠĪPQMNµÄĆ껿·ÖĪŖ1£ŗ3Į½²æ·Ö£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
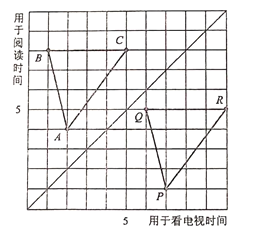
”¾ĢāÄæ”æĶ¼ÖŠ,µćA,B,C,P,Q,RĻŌŹ¾ĮĖ6ĆūŃ§ÉśĘ½¾łĆæÖÜÓĆÓŚŌĶĮæĪĶāŹéµÄŹ±¼äŗĶÓĆÓŚæ“µēŹÓµÄŹ±¼ä(µ„Ī»:h)
(1)ÓĆÓŠŠņŹż¶Ō±ķŹ¾Ķ¼ÖŠµćA,B,C,P,Q,R
(2)Ķ¼ÖŠ·½øńÖ½µÄ¶Ō½ĒĻßµÄ×óÉĻ·½µÄµćÓŠŹ²Ć“¹²Ķ¬µÄĢŲµć?ĖüÓŅĻĀ·½µÄµćÄŲ?
(3)Čż½ĒŠĪABCµÄĶ¼ŠĪ¾¹żŌõŃłµÄ±ä»»ŗóµĆµ½Čż½ĒŠĪPQRµÄĶ¼ŠĪ?ĘäÖŠµćA¶ŌÓ¦µćP,µćB¶ŌÓ¦µćQ,µćC¶ŌÓ¦µćR
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷øł¾ŻŃ§Ļ°ŗÆŹżµÄ¾Ń飬¶ŌŗÆŹż![]() µÄĶ¼ĻńÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ£®Ēė²¹³äĶźÕū£ŗ
µÄĶ¼ĻńÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ£®Ēė²¹³äĶźÕū£ŗ
£Ø1£©ĻČĢī±ķ£¬ŌŁŌŚČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĆčČ«±ķÖŠø÷¶Ō¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬²¢»³öøĆŗÆŹżµÄĶ¼Ļń£ŗ
x | ” | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | ” |
| ” | 2 |
| 3 | -3 |
| 0 | ” |
£Ø2£©½įŗĻŗÆŹżµÄĶ¼Ļń£¬Ėµ³öĮ½Ģõ²»Ķ¬ĄąŠĶµÄŠŌÖŹ£»
¢Ł________________________________£»____________________________________£®
¢Ś![]() µÄĶ¼ĻńŹĒÓÉ
µÄĶ¼ĻńŹĒÓÉ![]() µÄĶ¼ĻńČēŗĪĘ½ŅʵƵ½£æ
µÄĶ¼ĻńČēŗĪĘ½ŅʵƵ½£æ
___________________________________________£®
£Ø3£©µ±ŗÆŹżÖµ![]() Ź±£¬xµÄȔֵ·¶Ī§ŹĒ____________span>£®
Ź±£¬xµÄȔֵ·¶Ī§ŹĒ____________span>£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
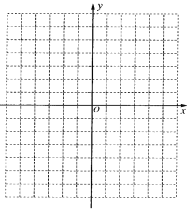
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ĆæŅ»øöŠ”·½øńµÄ±ßøö³¤ĪŖ1øöµ„Ī»£®

£Ø1£©ĒėŠ“³ö”÷ABCø÷µćµÄ×ų±ź£»
£Ø2£©Čō°Ń”÷ABCĻņÉĻĘ½ŅĘ2øöµ„Ī»£¬ŌŁĻņÓŅĘ½ŅĘ2øöµ„Ī»µĆµ½”÷A1B1C1£¬ŌŚĶ¼ÖŠ»³ö”÷A1B1C1£»
£Ø3£©Ēó”÷A1B1C1µÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
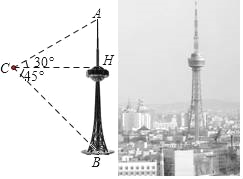
”¾ĢāÄæ”æ¼ŖĮÖŹ”¹ć²„µēŹÓĖž£Ø¼ņ³Ę”°¼ŖĖž”±£©ŹĒĪŅŹ”ÄæĒ°×īøßµÄČĖ¹¤½ØÖž£¬Ņ²ŹĒø©ī«³¤“ŗŹŠĆĄ¾°µÄ×ī¼ŃČ„“¦£®Ä³æĘ¼¼ŠĖȤŠ”×éĄūÓĆĪŽČĖ»ś“īŌŲ²āĮæŅĒĘ÷²āĮæ”°¼ŖĖž”±µÄøß¶Č£®ŅŃÖŖČēĶ¼½«ĪŽČĖ»śÖĆÓŚ¾ąĄė”°¼ŖĖž”±Ė®Ę½¾ąĄė138Ć׵ĵćC“¦£¬Ōņ“ÓĪŽČĖ»śÉĻ¹Ū²āĖž¼āµÄŃö½ĒĒ”ĪŖ30”ć£¬¹Ū²āĖž»ł×łÖŠŠÄµćµÄø©½ĒĒ”ĪŖ45”ć£®Ēó”°¼ŖĖž”±µÄøß¶Č£®£Ø×¢£ŗ ![]() ”Ö1.73£¬½į¹ū±£ĮōÕūŹż£©
”Ö1.73£¬½į¹ū±£ĮōÕūŹż£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
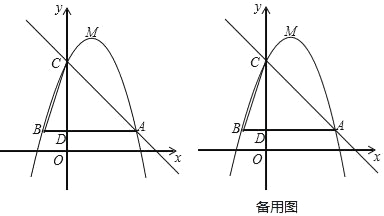
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹży=©x2+bx+c£ØĘäÖŠb£¬cĪŖ³£Źż£©µÄĶ¼Ļó¾¹żµćA£Ø3£¬1£©£¬µćC£Ø0£¬4£©£¬¶„µćĪŖµćM£¬¹żµćA×÷AB”ĪxÖį£¬½»yÖįÓŚµćD£¬½»øƶž“ĪŗÆŹżĶ¼ĻóÓŚµćB£¬Į¬½įBC£®
£Ø1£©Ēóøƶž“ĪŗÆŹżµÄ½āĪöŹ½¼°µćMµÄ×ų±ź£®
£Ø2£©Čō½«øƶž“ĪŗÆŹżĶ¼ĻóĻņĻĀĘ½ŅĘm£Øm£¾0£©øöµ„Ī»£¬Ź¹Ę½ŅĘŗóµĆµ½µÄ¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶„µćĀäŌŚ”÷ABCµÄÄŚ²æ£Ø²»°üĄØ”÷ABCµÄ±ß½ē£©£¬ĒómµÄȔֵ·¶Ī§£®
£Ø3£©ŃŲÖ±ĻßAC·½ĻņĘ½ŅĘøƶž“ĪŗÆŹżĶ¼Ļó£¬Ź¹µĆCMÓėĘ½ŅĘĒ°µÄCBĻąµČ£¬ĒóĘ½ŅĘŗóµćMµÄ×ų±ź£®
£Ø4£©µćPŹĒÖ±ĻßACÉĻµÄ¶Æµć£¬¹żµćP×÷Ö±ĻßACµÄ“¹ĻßPQ£¬¼ĒµćM¹ŲÓŚÖ±ĻßPQµÄ¶Ō³ĘµćĪŖM”䣮µ±ŅŌµćP”¢A”¢M”¢M”äĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪŹ±£¬Ö±½ÓŠ“³öµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŌŚÕż·½ŠĪABCDÖŠ£¬FŹĒCD±ßÉĻŅ»µć£Ø²»ÓėC”¢DÖŲŗĻ£©£¬¹żµćD×÷DG”ĶBF½»BFŃÓ³¤ĻßÓŚµćG£®Į¬½ÓAG£¬½»BDÓŚµćE£¬½»CDÓŚµćM£¬Į¬½ÓEF£®ČōDG=4£¬AG=![]() £¬ŌņEFµÄ³¤ĪŖ____________£®
£¬ŌņEFµÄ³¤ĪŖ____________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ·½³Ģ£ŗx![]() ©2x©8=0£¬½ā¾öŅ»ĻĀĪŹĢā£ŗ
©2x©8=0£¬½ā¾öŅ»ĻĀĪŹĢā£ŗ
£Ø1£©²»½ā·½³ĢÅŠ¶Ļ“Ė·½³ĢµÄøłµÄĒéæö£»
£Ø2£©Ēė°“ŅŖĒó·Ö±š½āÕāøö·½³Ģ£ŗ¢ŁÅä·½·Ø£»¢ŚŅņŹ½·Ö½ā·Ø£®
£Ø3£©ÕāŠ©·½·Ø¶¼ŹĒ½«½ā ×Ŗ»ÆĪŖ½ā £»
£Ø4£©³¢ŹŌ½ā·½³Ģ£ŗ![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬CD”ĶABÓŚµćD£¬CEŹĒ”ĻACBµÄĘ½·ÖĻߣ¬”ĻA£½20”ć,”ĻB£½60”ć£¬Ēó”ĻBCDŗĶ”ĻECDµÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com