
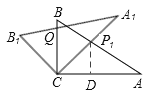
【题目】(2013年四川自贡12分)将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.

(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.
【答案】解答:(1)证明:∵∠B1CB=45°,∠B1CA1=90°,∴∠B1CQ=∠BCP1=45°。
∵在△B1CQ和△BCP1中, ,
,
∴△B1CQ≌△BCP1(ASA)。∴CQ=CP1。
(2)如图,过点P1作P1D⊥CA于D,
∵∠A=30°,∴P1D=![]() AP1=1。
AP1=1。
∵∠P1CD=45°,∴![]() 。.
。.
∴CP1=![]() P1D=
P1D=![]() 。
。
又∵CP1=CQ,∴CQ=![]() 。
。
(3)∵∠P1BE=90°,∠ABC=60°,∴∠A=∠CBE=30°。∴AC=、![]() BC 。
BC 。
由旋转的性质可得:∠ACP1=∠BCE,∴△AP1C∽△BEC。∴AP1:BE=AC:BC=![]() :1。
:1。
设AP1=x,则BE=![]() x,
x,
在Rt△ABC中,∠A=30°,∴AB=2BC=2。
∴![]() 。
。
∵![]() ,∴当x=1时,S△P1BE(max)=
,∴当x=1时,S△P1BE(max)=![]() 。
。
【解析】(1)先判断∠B1CQ=∠BCP1=45°,利用ASA即可证明△B1CQ≌△BCP1,从而得出结论。
(2)过点P1作P1D⊥CA于D,在RtADP1中,求出P1D,在Rt△CDP1中求出CP1,继而可得出CQ的长度。
(3)证明△AP1C∽△BEC,则有AP1:BE=AC:BC=![]() :1,设AP1=x,则BE=
:1,设AP1=x,则BE=![]() x,得出S△P1BE关于x的表达式,利用配方法求最值即可。
x,得出S△P1BE关于x的表达式,利用配方法求最值即可。


科目:初中数学 来源: 题型:
【题目】如图, 在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上
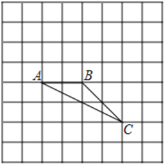
(1) 填空∠ABC=___________
(2) 若点A在网格所在的坐标平面内的坐标为(1,-2),请建立平面直角坐标系,D是平面直角坐标系中一点,并作出以A、B、C、D四个点为顶点的平行四边形,直接写出满足条件的D点的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
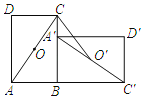
【题目】如图,在矩形ABCD中,O是对角线AC的中点.将ABCD绕点B顺时针旋转90°.旋转后的四边形为A'B′C′D',点A,C,D,O的对应点分别为A′,C',D',O’,若AB=8,BC=10,则线段CO’的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作图
在下面的网格中,已知△ABC的顶点分别落在网格的格点,点A′、C′分别是点A、C两点绕某一点O旋转同样的角度后的对应点.
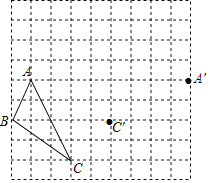
(1)请在下图中作出旋转中心O的位置;
(2)点A′是点A绕点O旋转 度形成的;
(3)画出△ABC绕点O旋转同样的角度后的△A′B'C’.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=105°,AC边上的垂直平分线交AB边于点D,交AC边于点E,连结CD.
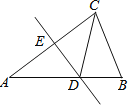
(1)若AB=10,BC=6,求△BCD的周长;
(2)若AD=BC,试求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小丽设计了A、B两种游戏:游戏A的规则是:用3张数字分别是2、3、4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字,若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.游戏B的规则是:用4张数字分别是5、6、8、8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌,若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜,否则小丽获胜.请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com