练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．按要求完成下列各小题．
    （1）计算：-33+5×（-$\frac{8}{5}$）-（-4）2÷（-8）
    （2）写出如图所示的几何体有几条棱，几个顶点．

    分析 （1）根据有理数的运算，可得答案；
    （2）根据棱柱的特性，可得答案．

    解答 解：（1）原式=-27+（-8）+2=-33；
          （2）三棱柱有9条棱；6个顶点．

    点评 本题考查了有理数的混合运算，正确利用有理数的运算是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．如图，△ABC和△ADE均为等腰直角三角形，∠ACB=∠ADE=90°，连接BE，F为BE的中点，连接DF，CF．
    （1）如图①，当边AD与边AB重合时，求证：DF=CF，DF⊥CF；
    （2）将△ADE绕A点旋转到如图②位置时，（1）中的结论还成立吗，判断并说明理由；
    （3）如图③，若∠BAE=135°，AC=2$\sqrt{2}$，AD=1，则CF的长为$\frac{\sqrt{10}}{2}$（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．在平面直角坐标系中，点P（-2，a）与点Q（b，3）关于原点对称，则b3的值为（　　）
    A．-$\frac{1}{8}$B．$\frac{1}{8}$C．-8D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

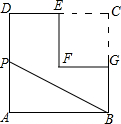    13．如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致为（　　）
    A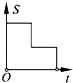．B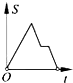．C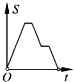．D．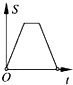

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

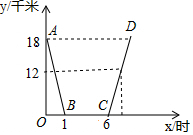    20．10月2日早晨8点，小华和同学骑自行车去净月潭游玩，当天按原路返回，如图，是小华出行的过程中，他距净月潭的距离y（千米）与他离开家的时间x（小时）之间的函数图象．
    （1）小华去时骑自行车的速度是18千米/小时；
    （2）求线段AB所表示的函数关系式；
    （3）已知下午2点48分时，小华距净月潭12千米，求线段CD所表示的函数关系式，并求他何时到家．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．下面给出的算式中，你认为可以帮助探究有理数加法法则的算式组合是②③⑤⑥⑦⑧．
    ①3+（-2）；②4+3；③（-3）+（-2）；④3+13；⑤3+0；⑥6+（-3）；⑦4+（-5）；⑧5+（-5）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

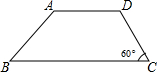    17．如图，一条公路路基的横断面是梯形（AD∥BC），路基顶宽AD=8米，高3米，斜坡AB的坡度为i=1：1，斜坡DC的坡角∠C=60°．
    （1）求斜坡AB的坡角∠B的度数；
    （2）求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若不等式组$\left\{\begin{array}{l}{x≥a}\\{x＜2}\end{array}\right.$有解，则a的取值范围是a＜2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知函数y=$\frac{k}{x}$的图象经过点A（-2，4）．
    （1）求k的值；
    （2）当x取什么值时，函数的值大于0？

    查看答案和解析>>

    同步练习册答案