
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C,且OC=2OA,抛物线的对称轴x轴交于点D.
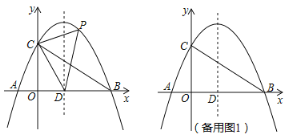
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上位于对称轴右侧的一个动点,设点P点的横坐标为m,且S△CDP=![]() S△ABC,求m的值;
S△ABC,求m的值;
(3)K是抛物线上一个动点,在平面直角坐标系中是否存在点H,使B、C、K、H为顶点的四边形成为矩形?若存在,直接写出点H的坐标;若不存在,说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)m1=4或m2=
x+4;(2)m1=4或m2=![]() ;(3)点H坐标为(6,﹣4),(6,﹣2),(﹣18,﹣32).
;(3)点H坐标为(6,﹣4),(6,﹣2),(﹣18,﹣32).
【解析】
(1)结合A(﹣2,0),B(8,0)由两点式可得抛物线解析式为y=a(x+2)(x﹣8),求出点C坐标,代入即可求出抛物线解析式;
(2)点P在抛物线上,可设P(m,﹣![]() m2+
m2+![]() m+4),结合C点坐标可得直线PC的解析式,已知直线与对称轴交点E的坐标,DE长可知,根据S△ABC=
m+4),结合C点坐标可得直线PC的解析式,已知直线与对称轴交点E的坐标,DE长可知,根据S△ABC=![]() ×AB×OC求出其面积,由题中条件可知△CDP的面积,由三角形面积公式可得m的值;
×AB×OC求出其面积,由题中条件可知△CDP的面积,由三角形面积公式可得m的值;
(3)分类讨论,①若BC为边,∠CBK=90°时,将BC绕点B逆时针旋转90°得到BC',根据AAS证明△BCO≌△BC'E,依据全等的性质可得点B点C的坐标,求出直线BC的表达式与抛物线的解析式联立求解可得点K横坐标,由矩形的性质可知xC﹣xB=xH﹣xK,![]() ,结合点B、C、D点坐标可得H点坐标.②若BC为边,∠BCK=90°时,同理可求:直线CK的解析式,与抛物线的解析式联立求解可得点K横坐标,同理可得H点坐标;③若BC为对角线,由B点C点坐标可得BC的中点坐标及BC的长,点K在抛物线上,设设点K(x,﹣
,结合点B、C、D点坐标可得H点坐标.②若BC为边,∠BCK=90°时,同理可求:直线CK的解析式,与抛物线的解析式联立求解可得点K横坐标,同理可得H点坐标;③若BC为对角线,由B点C点坐标可得BC的中点坐标及BC的长,点K在抛物线上,设设点K(x,﹣![]() x2+
x2+![]() x+4),利用勾股定理可求出x的值,选择符合题意的,求出点K坐标后结合KH的中点坐标可知H点坐标,综上所述,点H的坐标有3种情况.
x+4),利用勾股定理可求出x的值,选择符合题意的,求出点K坐标后结合KH的中点坐标可知H点坐标,综上所述,点H的坐标有3种情况.
(1)∵A(﹣2,0),B(8,0)
∴OA=2,OB=8,
∵OC=2OA,
∴OC=4,
∴点C(0,4)
∵设y=a(x+2)(x﹣8)经过点C,
∴4=﹣16a,
∴a=﹣![]() ,
,
∴抛物线解析式为:y=﹣![]() (x+2)(x﹣8)=﹣
(x+2)(x﹣8)=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)如图1,
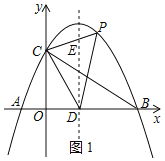
由题意:点D(3,0),
∴OD=3,
设P(m,﹣![]() m2+
m2+![]() m+4),(m>0,﹣
m+4),(m>0,﹣![]() m2+
m2+![]() m+4>0)
m+4>0)
∵C(0,4),
∴直线PC的解析式可表示为:y=(﹣![]() m+
m+![]() )x+4,
)x+4,
设直线PC与对称轴的交点为E,则点E(3,﹣![]() m+
m+![]() ),
),
∴DE=﹣![]() m+
m+![]() ,
,
∵S△ABC=![]() ×AB×OC,
×AB×OC,
∴S△ABC=![]() ×10×4=20,
×10×4=20,
∵S△CDP=![]() S△ABC,
S△ABC,
∴![]() ×(﹣
×(﹣![]() m+
m+![]() )×m=
)×m=![]() ×20,
×20,
∴m1=4或m2=![]() ;
;
(3)若BC为边,∠CBK=90°时,如图2,将BC绕点B逆时针旋转90°得到BC',
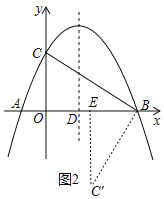
∴BC=BC',∠CBC'=90°,
∴∠CBO+∠C'=90°,∠CBO+∠OCB=90°,
∴∠OCB=∠EBC',且BC=BC',∠BEC'=∠BOC=90°,
∴△BCO≌△BC'E(AAS)
∴BE=OC=4,OB=EC'=8,
∴点C'(4,﹣8),且B(8,0)
∴直线BC'解析式为:y=2x﹣16,
∴2x﹣16=﹣![]() x2+
x2+![]() x+4,
x+4,
∴x1=﹣10,x2=8,
∴点K(﹣10,﹣36),
∵xC﹣xB=xH﹣xK,
∴0﹣8=xH﹣(﹣10),
∴xH=﹣18,
∵![]() ,
,
∴yH=﹣32,
∴点H(﹣18,﹣32),
若BC为边,∠BCK=90°时,
同理可求:直线CK的解析式为:y=2x+4,
∴2x+4=﹣![]() x2+
x2+![]() x+4,
x+4,
∴x1=﹣2,x2=0,
∴点K坐标(﹣2,0)
∵![]() ,
,
∴0﹣8=﹣2﹣xH,
∴xH=﹣6,
∵![]() ,
,
∴yH=﹣4,
∴点H(6,﹣4),
若BC为对角线,
∵B、C、K、H为顶点的四边形成为矩形,
∴BC=KH,BC与KH互相平分,
∵B(8,0),C(0,4)
∴BC中点坐标(4,2),BC=![]() =
=![]() =4
=4![]() ,
,
设点K(x,﹣![]() x2+
x2+![]() x+4)
x+4)
∴(x﹣4)2+(﹣![]() x2+
x2+![]() x+4﹣2)2=(2
x+4﹣2)2=(2![]() )2,
)2,
∴x(x﹣2)2(x﹣8)=0,
∴x1=0,x2=2,x3=8,
∴K(2,6),且KH的中点坐标(4,2),
∴点H(6,﹣2)
综上所述:点H坐标为(6,﹣4),(6,﹣2),(﹣18,﹣32).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过
过![]() ,
,![]() 两点.
两点.
备用图1 备用图2
(1)求该抛物线的解析式;
(2)点![]() 是抛物线上一点,且位于第一象限,当
是抛物线上一点,且位于第一象限,当![]() 的面积为6时,求点
的面积为6时,求点![]() 的坐标;
的坐标;
(3)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?存在,求出点
两部分?存在,求出点![]() 的坐标;不存在,请说明理由.
的坐标;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=6cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以![]() cm/s的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为t(s)
cm/s的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为t(s)
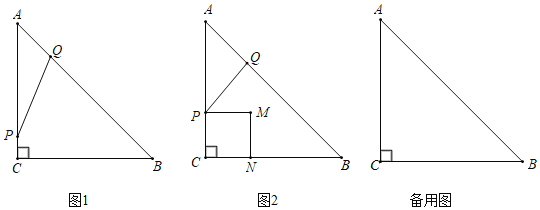
(1)当t=3时,线段PQ的长为 cm;
(2)是否存在某一时刻t,使点B在线段PQ的垂直平分线上?若存在,求出t的值;若不存在,请说明理由;
(3)如图2,以PC为边,往CB方向作正方形CPMN,设四边形CPMN与Rt△ABC重叠部分的面积为S,求S关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丰都县某中学为培养学生综合实践能力,开展了一系列综合实践活动,有一次财商训练活动中,小明同学准备去集市批发两种商品用于活动中交易.预先了解到A、B两种商品的价格之和为27元,小明计划购买B商品的数量比A商品的数量多2件,但一共不超过25件,且每样不少于3件,但小明去购买时发现A商品正打九折销售,而B商品的价格提高了20%,小明决定将A、B产品的购买数量对调,这样实际花费只比计划多8元,已知价格和购买数量均为整数,则小明购买两种商品实际花费为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的等腰直角三角形按如图方式放置在平面直角坐标系中,OA在x轴上,已知∠COD=∠OAB=90°,OC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求k的值.
(2)把△OCD沿射线OB移动,当点D落在y=![]() 图象上时,求点D经过的路径长.
图象上时,求点D经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于给定函数y=a1x2+b1x+c1(其中a1、b1、c1为常数,且a1≠0),则称函数y= (a1=a2,b1+b2=0,c1+c2=0)为函数y=a1x2+b1x+c1(其中a1,b1,c1为常数,且a1≠0)的“相关函数”,此“相关函数”的图象记为G.
(a1=a2,b1+b2=0,c1+c2=0)为函数y=a1x2+b1x+c1(其中a1,b1,c1为常数,且a1≠0)的“相关函数”,此“相关函数”的图象记为G.
(1)已知函数y=﹣x2+4x+2.
①直接写出这个函数的“相关函数”;
②若点P(a,1)在“相关函数”的图象上,求a的值;
③若直线y=m与图象G恰好有两个公共点,直接写出m的取值范围;
(2)设函数y=﹣![]() x2+nx+1(n>0)的相关函数的图象G在﹣4≤x≤2上的最高点的纵坐标为y0,当
x2+nx+1(n>0)的相关函数的图象G在﹣4≤x≤2上的最高点的纵坐标为y0,当![]() ≤y0≤9时,直接写出n的取值范围.
≤y0≤9时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由;
若过O点的直线旋转至图(2)、(3)的情况,其余条件不变,那么图(1)中的∠1与∠2的关系成立吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com