
【题目】某礼品制造工厂接受一批玩具的订货任务,按计划天数生产,如果每天生产 20 个玩具,则比订货任务少 100 个;如果每天生产 23 个玩具,则可以超过订货任务 20 个,请求出这批玩具的订货任务是多少个,原计划几天完成任务.
A. 40,800 B. 40,900 C. 50,800 D. 50,900
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边BC、CD上的点,![]() =
=![]() ,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.
,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.
(1)若正方形的边长为4,则EG等于 ;
(2)求证:△ECF∽△FDA;
(3)比较∠EAB与∠EAF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P在第三象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为( )
A.(3,5)
B.(-5,3)
C.(3,-5)
D.(-5,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
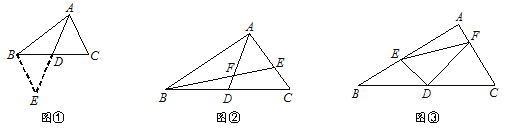
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队计划在10天内修路6km.现计划发生变化,准备8天完成修路任务,那么这8天平均每天至少要修路多少?设这8天平均每天要修路xkm,依题意得一元一次不等式为:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(5,2).
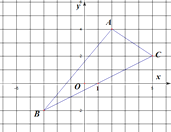
(1)在图中画出△ABC关于y轴对称的△A′B′C′,并写出点A′,B′,C′的坐标;
(2)求△ABC的面积;
(3)在x轴上找点P,使PA+PC的值最小,并观察图形,写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题①不相交的直线是平行线;②矩形的对角线相等且互相平分;③同位角相等;④平行四边形既是中心对称图形又是轴对称图形;⑤同圆中同弦所对的圆周角相等.其中正确的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com