
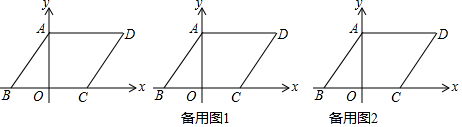
分析 (1)根据平方和算术平方根的非负性列式得:OA=4,OB=3,则A(0,4),B(-3,0),根据平行四边形的对边相等得出C的坐标;
(2)如图1,利用三角形的内角和得:∠PCO=∠OAB,由等角的三角函数列式可求OP的长,写出P的坐标;
(3)如图2,作辅助线,构建菱形AMCN,设AM=x,则OM=4-x,由勾股定理求x的值,则AM=CM=$\frac{25}{8}$,OM=$\frac{7}{8}$,分别求出NH和OH的长,写出N的坐标,利用待定系数法求直线DN的解析式,判断点P与直线DN的位置关系.
解答 解:(1)∵$\sqrt{OA-4}+(OB-3)^{2}=0$,
∴OA-4=0,OB-3=0,
∴OA=4,OB=3,
∴A(0,4),B(-3,0),
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∴OC=6-3=3,
∴C(3,0);
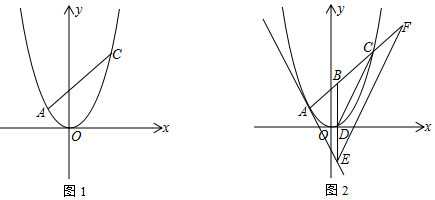
(2)如图1,延长CP交AB于G,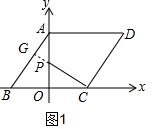
∴∠AGP=∠COP=90°,
∵∠APG=∠OPC,
∴∠PCO=∠OAB,
tan∠PCO=tan∠OAB=$\frac{OP}{OC}=\frac{OB}{OA}$,
∴$\frac{OP}{3}=\frac{3}{4}$,
∴OP=$\frac{9}{4}$,
∴P(0,$\frac{9}{4}$); 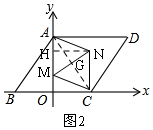
(3)如图2,作AC的中垂线MN,交y轴于M,交AC于G,根据菱形AMCN,则AM=CM,
设AM=x,则OM=4-x,
在Rt△COM中,由勾股定理得:x2=(4-x)2+32,
∴x=$\frac{25}{8}$,
∴AM=CM=$\frac{25}{8}$,
∵AC=5,
∴AG=CG=$\frac{5}{2}$,
∴MG=$\sqrt{(\frac{25}{8})^{2}-(\frac{5}{2})^{2}}$=$\frac{15}{8}$,
∴MN=2MG=$\frac{15}{4}$,
∵四边形AMCN是菱形,
∴∠CMN=∠AMN,
过N作NH⊥y轴于H,
cos∠AMN=cos∠CMN=$\frac{MH}{MN}=\frac{MG}{MC}$,
∴$\frac{MH}{\frac{15}{4}}=\frac{\frac{15}{8}}{\frac{25}{8}}$,
∴MH=$\frac{9}{4}$,
由勾股定理得:NH=$\sqrt{M{N}^{2}-M{H}^{2}}$=$\sqrt{(\frac{15}{4})^{2}-(\frac{9}{4})^{2}}$=3,
OM=4-$\frac{25}{8}$=$\frac{7}{8}$,
∴OH=$\frac{7}{8}$+$\frac{9}{4}$=$\frac{25}{8}$,
∴N(3,$\frac{25}{8}$);
设直线DN的解析式为:y=kx+b,
把D(5,4)和N(3,$\frac{25}{8}$)代入得:$\left\{\begin{array}{l}{5k+b=4}\\{3k+b=\frac{25}{8}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{7}{16}}\\{b=\frac{29}{16}}\end{array}\right.$,
∴直线DN的解析式为:y=$\frac{7}{16}$x+$\frac{29}{16}$,
∵P(0,$\frac{9}{4}$);
∴P在直线DN外.
点评 本题考查了平行四边形和菱形的性质,同时考查了坐标与图形特点、二次根式与平方的非负性、三角函数、利用待定系数法求一次函数的解析式,难度适中,答题时注意看清题意.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
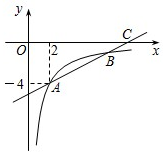 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
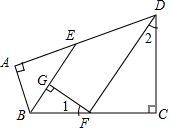 如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com