
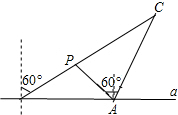
 在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号).
在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号). 分析 作AD⊥BC于点D.先根据方向角的定义得出∠PBA=∠PAB=30°,那么AP=PB=20海里,由三角形外角的性质得出∠APD=∠PBA+∠PAB=60°.再解Rt△ADP,求出AD=PA•sin∠APD=20•sin60°=10$\sqrt{3}$海里.由∠BAC=90°+15°=105°,根据三角形内角和定理得到∠C=180°-∠ABC-∠BAC=45°.然后解Rt△ADC中,即可求出AC=$\frac{AD}{sin∠C}$=10$\sqrt{6}$海里.
解答 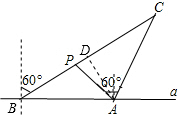 解:作AD⊥BC于点D.
解:作AD⊥BC于点D.
∵∠PBA=∠PAB=90°-60°=30°,
∴AP=PB=20海里,
∴∠APD=∠PBA+∠PAB=60°.
在Rt△ADP中,∵∠ADP=90°,
∴AD=PA•sin∠APD=20•sin60°=10$\sqrt{3}$海里.
∵∠BAC=90°+15°=105°,
∴∠C=180°-∠ABC-∠BAC=45°.
在Rt△ADC中,∵∠ADC=90°,
∴AC=$\frac{AD}{sin∠C}$=10$\sqrt{6}$海里.
答:AC间的距离是10$\sqrt{6}$海里.
点评 本题考查了解直角三角形的应用-方向角问题,等腰三角形的判定,三角形内角和定理及外角的性质,锐角三角函数的定义,准确作出辅助线构造直角三角形是解题的关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3+a2=2a5 | B. | (2ab2)3=6a3b6 | ||
| C. | 2a2b•3ab2=6a2b3 | D. | x3y2÷(-2x2y)=-$\frac{1}{2}$xy |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为$\sqrt{6}$.
如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
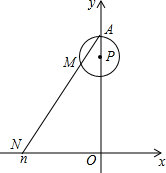 如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1,点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0).设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{3}$变化到$\frac{2}{3}$时,点N相应移动的路经长为$\frac{2}{3}\sqrt{3}$.
如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1,点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0).设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{3}$变化到$\frac{2}{3}$时,点N相应移动的路经长为$\frac{2}{3}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com