
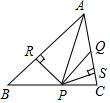
 如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )| A. | 全部正确 | B. | 仅①正确 | C. | 仅①、②正确 | D. | 仅①、③正确 |
分析 只要证明Rt△APR≌Rt△APS,推出AS=AR,∠PAR=∠PAS,故①正确,由AQ=PQ,推出∠PAS=∠APQ,推出∠PAR=∠APQ,推出PQ∥AR,故②正确,在△BRP和△CSP中,只有一个角,一条边相等无法证明全等.故③错误.
解答 解:∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
在Rt△APR和Rt△APS中,
$\left\{\begin{array}{l}{AP=AP}\\{PR=PS}\end{array}\right.$,
∴Rt△APR≌Rt△APS,
∴AS=AR,∠PAR=∠PAS,故①正确,
∵AQ=PQ,
∴∠PAS=∠APQ,
∴∠PAR=∠APQ,
∴PQ∥AR,故②正确,
在△BRP和△CSP中,只有一个角,一条边相等无法证明全等.故③错误,
故选C.
点评 本题考查全等三角形的判定和性质、平行线的判定等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$
如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )| A. | 过一点有无数条直线 | |
| B. | 两点之间线段的长度,叫做这两点之间的距离 | |
| C. | 经过两点有且只有一条直线 | |
| D. | 两点之间,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 340+$\frac{2}{5}$ | B. | 340×(1+$\frac{2}{5}$) | C. | 340+340×$\frac{3}{5}$ | D. | 340×$\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
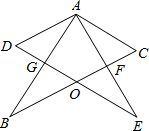 如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG=BG.其中正确的个数为( )
如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG=BG.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,动点P从D点开始沿DA以2cm/s的速度向A运动,动点Q从B点开始沿BC以1cm/s的速度向C运动,P、Q分别从D、B同时出发,当其中一点到端点时,另一点也随之停止运动,连结PQ,设运动时间为t.
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,动点P从D点开始沿DA以2cm/s的速度向A运动,动点Q从B点开始沿BC以1cm/s的速度向C运动,P、Q分别从D、B同时出发,当其中一点到端点时,另一点也随之停止运动,连结PQ,设运动时间为t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com