
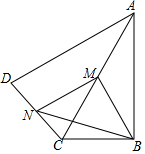
 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.分析 (1)根据直角三角形的性质得到BM=$\frac{1}{2}$AC,根据三角形中位线定理得到MN=$\frac{1}{2}$AD,根据题意证明;
(2)证明△NMB是等腰直角三角形,根据勾股定理计算即可.
解答 (1)证明:∵∠ABC=90°,M为AC中点,
∴BM=$\frac{1}{2}$AC,
∵M为AC中点,N为DC中点,
∴MN=$\frac{1}{2}$AD,
∵AD=AC,
∴BM=MN;
(2)解:∵∠BAD=60°,AC平分∠BAD,
∴∠DAC=∠CAB=30°,
∴BM=AM=$\frac{1}{2}$AC=1,
∴∠MAB=∠MBA=30°,
∴∠CMB=60°
根据三角形中位线定理得,MN∥AD,MN=$\frac{1}{2}$AD=1,
∴∠DAC=∠NMC=30°,
∴△NMB是等腰直角三角形,
由勾股定理得,BN=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$..
点评 本题考查的是直角三角形的性质、三角形中位线定理以及等腰三角形的性质,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.


科目:初中数学 来源: 题型:解答题
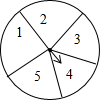 如图,有一个可以自由转动的转盘,被均匀分成5等份,分别标上1、2、3、4、5五个数字.甲乙两人玩一个游戏,其规则如下:任意转动转盘一次,转盘停止后,指针指向一个数字,如果所得的数字是偶数,则甲胜;如果所得的数字是奇数,则乙胜.
如图,有一个可以自由转动的转盘,被均匀分成5等份,分别标上1、2、3、4、5五个数字.甲乙两人玩一个游戏,其规则如下:任意转动转盘一次,转盘停止后,指针指向一个数字,如果所得的数字是偶数,则甲胜;如果所得的数字是奇数,则乙胜.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 628ml | B. | 603ml | C. | 588ml | D. | 568ml |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x•(-xy)2=-2x3y | B. | (-x2)3÷(-x3)2=1 | ||
| C. | ($\frac{3}{4}$a3-$\frac{1}{2}$b)•2ab=$\frac{3}{2}$a4b-ab2 | D. | (3m-1)2=9m2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
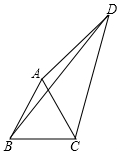 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )| A. |  | B. |  | C. | 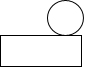 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com