
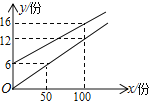
【题目】武汉市某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示
(1) 求甲、乙两种收费方式的函数关系式;
(2) 当印刷多少份学案时,两种印刷方式收费一样?
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
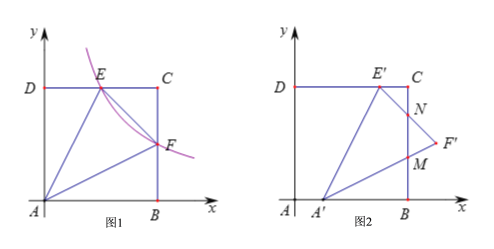
【题目】如图1,正方形ABCD的边长为4,以AB所在的直线为x轴,以AD所在的直线为y轴建立平面直角坐标系![]() 反比例函数
反比例函数![]() 的图象与CD交于E点,与CB交于F点.
的图象与CD交于E点,与CB交于F点.
(1)求证:![]() ;
;
(2)若![]() 的面积为6,求反比例函数的解析式;
的面积为6,求反比例函数的解析式;
(3)在(2)的条件下,将![]() 沿x轴的正方向平移1个单位后得到
沿x轴的正方向平移1个单位后得到![]() ,如图2,线段
,如图2,线段![]() 与
与![]() 相交于点M,线段
相交于点M,线段![]() 与BC相交于点N.求
与BC相交于点N.求![]() 与正方形ABCD的重叠部分面积.
与正方形ABCD的重叠部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
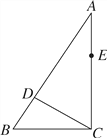
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
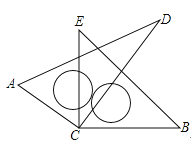
【题目】如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.
(1)如图1,若∠1=60°,求∠2,∠3的度数.

(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD请阅读下面的解答过程并填空(理由或数学式)
解:如图2,过点P作MN∥AB
则∠EPM=∠PEB(_______)
∵AB∥CD(已知)MN∥AB(作图)
∴MN∥CD(_______)
∴∠MPF=∠PFD (_______)
∴_____=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
②拓展应用,当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=_____度.
③当点P在图4的位置时,请直接写出∠EPF,∠PEB,∠PFD三个角之间关系_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
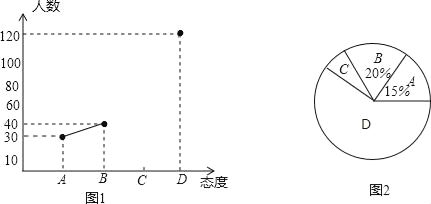
【题目】中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了市区某校七年级若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).统计员在将测试数据绘制成图表时发现,反对漏统计6人,赞成漏统计4人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
家长对中学生带手机上学各项态度人数统计表和统计图:
态度 | 调整前人数 | 调整后人数 |
A.无所谓 | 30 | 30 |
B.基本赞成 | 40 | 40 |
C.赞成 | ||
D.反对 | 114 | 120 |
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)填写统计表,并根据调整后数据补全折线统计图;
(3)根据抽样调查结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商家常将两种糖混合成“什锦糖”出售.对“什锦糖”的定价用以下方法确定:
若A种糖的单价为a元/千克,B种糖的单价为b元/千克(a≠b),则m千克的A种糖与n千克的B种糖混合而成的“什锦糖”单价为![]() 元.
元.
(1)当a=20,b=30时,
①将10千克的A种糖与15千克的B种糖混合而成的“什锦糖”单价为多少?
②在①的基础上,若要将“什锦糖”单价提高2元,则需增加B种糖多少千克?
(2)若现有两种“什锦糖”:一种是由10千克的A种糖和10千克的B种糖混合而成,另一种是由100元价值的A种糖和100元价值的B种糖混合而成,则这两种“什锦糖”的单价哪一种更大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣2与x轴交于A,B两点(点A在点B的右边),与y轴交于点C.
x﹣2与x轴交于A,B两点(点A在点B的右边),与y轴交于点C.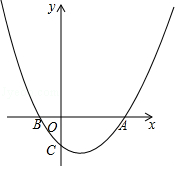
(1)求点A,B,C的坐标;
(2)点D是此抛物线上的点,点E是其对称轴上的点,求以A,B,D,E为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点P,使得△ACP是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.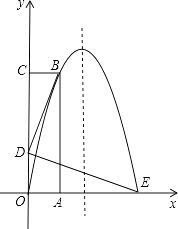
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com