Question

17．如图1，矩形ABCD中AB=6$\sqrt{3}$，∠CAB=30°，Rt△EFG的边FG在CA延长线上，点G与A重合，∠EFG=90°，EF=3，∠E=30°；将矩形ABCD固定，把Rt△EFG沿着射线AC方向按每秒1单位运动，知道点G与C重合时停止运动，设Rt△EFG的运动时间是t（t＞0）．
（1）求出当点E恰好落在DC上时，运动时间t的值；
（2）在整个运动过程中，设Rt△EFG与△ACD的重合部分面积为S，当t$＞\sqrt{3}$时，求出满足S=$\frac{2}{3}$S_△EFG的相应的t的值；
（3）如图2，当点E恰好落在DC上时，将△EFC绕点F顺时针旋转α°（0＜α＜180），记旋转中的△EFC为△E′FC′，在旋转过程中，设直线E′C′与直线AC交于N，与直线AB交于M，是否存在这样的M、N两点，使△AMN为等腰三角形？若存在求出此时FN的值；若不存在，请说明理由．

Answer 1

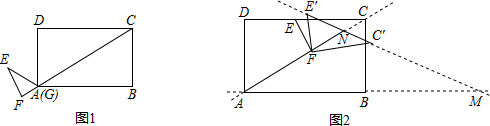
分析 （1）先由三角函数求AE和AC的长，则AG′=AC-G′C=AC-AE，求出AG′，因为速度为每秒1单位，求出时间t；
（2）作辅助线，由S=$\frac{2}{3}$S_△EFG可知：四边形MNF′G′的面积是△EFG面积的三分之二，得△E′MN的面积是△EFG面积的$\frac{1}{3}$，先求△EFG面积，再利用t表示△E′MN的面积，代入即可求出t的值；
（3）分四种情形①如图3中，当NA=NM时，②如图4中，当AN=AM时，③如图6中，当MA=MN时，④如图7中，当AN=AM时，分别求解即可．

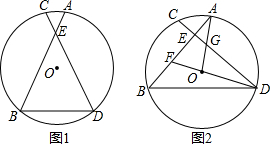
解答 解：（1）如图1中，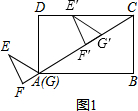

Rt△EFG中，EF=3，∠E=30°，
∴cos30°=$\frac{EF}{EG}$，
∴EG=$\frac{EF}{cos30°}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$，
∴E′G′=EG=2$\sqrt{3}$，
在Rt△ABC中，AB=6$\sqrt{3}$，∠CAB=30°，
∴cos30°=$\frac{AB}{AC}$，
AC=$\frac{AB}{cos30°}$=$\frac{6\sqrt{3}}{\frac{\sqrt{3}}{2}}$=12，
∵DC∥AB，
∴∠DCA=∠CAB=30°，
∵∠E′G′F′=90°-30°=60°，
∴∠G′E′C=30°，
∴∠G′E′C=∠DCA，
∴G′C=G′E′=2$\sqrt{3}$，
∴AG′=AC-G′C=12-2$\sqrt{3}$，
∴t=12-2$\sqrt{3}$；

（2）当t=$\sqrt{3}$时，如图2，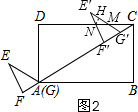

∵∠E′AF′=60°，AF′=$\sqrt{3}$
∴E′F′=tan60°×$\sqrt{3}$=$\sqrt{3}$×$\sqrt{3}$=3
∴点E′在AD上
如图2，过N作NH⊥E′G′，交E′G′于H
S_△DEF=$\frac{1}{2}$EF•FG=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$
由题意得：GG′=t，CG′=12-t
∵∠MG′F′=60°，∠DCA=30°
∴∠G′MC=30°
∴△MCG′是等腰三角形
∴G′M=CG′=12-t
∴E′M=2$\sqrt{3}$-（12-t）=2$\sqrt{3}$-12+t
同理得△E′NM也是等腰三角形
∵NH⊥E′G′
∴E′H=$\frac{1}{2}$E′M=$\frac{2\sqrt{3}-12+t}{2}$
∴HN=tan30°•E′H=$\frac{\sqrt{3}（2\sqrt{3}-12+t）}{6}$
根据S=$\frac{2}{3}$S_△EFG得：S_△E′MN=$\frac{1}{3}$S_△EFG，
则$\frac{1}{3}$×$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}$E′M•NH
$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$×（2$\sqrt{3}$-12+t）×$\frac{\sqrt{3}（2\sqrt{3}-12+t）}{6}$
解得：t₁=12-2$\sqrt{3}$+$\sqrt{6}$，t₂=12-2$\sqrt{3}$-$\sqrt{6}$
由题意得：$\sqrt{3}$＜t≤12，都符合条件，
∴t=12-2$\sqrt{3}$±$\sqrt{6}$；

（3）①如图3中，当NA=NM时，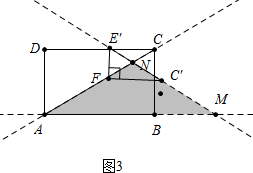

∵∠E′C′F=∠AMN=30°，
∴FC′∥AM，
∴∠NFC′=∠NAB=30°，
∴∠NFC′=∠NC′F=30°，
∴NF=NC′，∠NFE′=∠NE′F=60°，
∴FN=NE′，
∴FN=$\frac{1}{2}$E′C′=$\frac{1}{2}$×6=3．
②如图4中，当AN=AM时，作FG⊥E′C′于G，则FG=$\frac{3\sqrt{3}}{2}$，∠ANC=∠AMN=75°，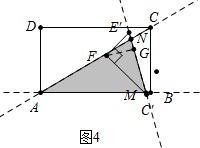

把△FNG放大如图5中，在FG上取一点H，使得FH=HN，则∠F=∠HNF=15°，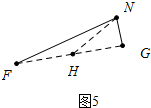

∴∠GHN=∠F+∠HNF=30°，设NG=x，则HN=HF=2x，GH=$\sqrt{3}$x，
∴2x+$\sqrt{3}$x=$\frac{3}{2}$$\sqrt{3}$，
∴x=3$\sqrt{3}$-$\frac{9}{2}$．
∴FN=$\sqrt{F{G}^{2}+N{G}^{2}}$=$\sqrt{（\frac{3\sqrt{3}}{2}）^{2}+（3\sqrt{3}-\frac{9}{2}）^{2}}$=$\frac{9\sqrt{2}}{2}$-$\frac{3\sqrt{6}}{2}$．
③如图6中，当MA=MN时，点N与点C重合，此时FN=FC=3$\sqrt{3}$．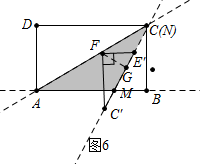

④如图7中，当AN=AM时，

把△FNG放大如图8中，在NG上取一点H，使得HN=HF．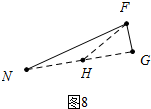

∵∠N=∠HFN=15°，
∴∠FHG=∠N+∠HFN=30°，
∵FG=$\frac{3\sqrt{3}}{2}$，
∴FH=NH=2FG=3$\sqrt{3}$，GH=$\frac{9}{2}$，
∴FN=$\sqrt{F{G}^{2}+G{N}^{2}}$=$\sqrt{（\frac{3\sqrt{3}}{2}）^{2}+（3\sqrt{3}+\frac{9}{2}）^{2}}$=$\frac{9\sqrt{2}}{2}$+$\frac{3}{2}$$\sqrt{6}$．

点评 本题考查四边形综合题、平移变换、旋转变换、等腰三角形的性质、勾股定理等知识，解题的关键是学会分类讨论，学会正确画出图形，学会添加常用辅助线，构造直角三角形，利用勾股定理解决求线段问题，属于中考压轴题．