
����Ŀ����ͼ����ֱ������ϵ�У�Rt��OAB��ֱ�Ƕ���A��x���ϣ�OA=4��AB=3������M�ӵ�A��������ÿ��1����λ���ȵ��ٶȣ���AO���յ�O�ƶ���ͬʱ��N�ӵ�O��������ÿ��1.25����λ���ȵ��ٶȣ���OB���յ�B�ƶ��������������˶���x�루0��x��4��ʱ������������⣺
��1�����N�����꣨�ú�x�Ĵ���ʽ��ʾ����
��2�����OMN�������S����S��x֮��ĺ�������ʽ����xΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3�������������˶������У��Ƿ����ijһʱ�̣�ʹ��OMN��ֱ�������Σ������ڣ����x��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��������ã�MA=x��ON=1.25x��
��Rt��OAB�У��ɹ��ɶ����ã�OB= ![]() =
= ![]() =5��
=5��
��NP��OA��P����ͼ1��ʾ��

��NP��AB��
���OPN�ס�OAB��
�� ![]() ��
��
�� ![]() ��
��
��ã�OP=x��PN= ![]() ��
��
���N�������ǣ�x�� ![]() ��
��
��2��
�⣺�ڡ�OMN�У�OM=4��x��OM���ϵĸ�PN= ![]() ��
��
��S= ![]() OMPN=
OMPN= ![]() ��4��x��
��4��x�� ![]() =��
=�� ![]() x2+
x2+ ![]() x��
x��
��S��x֮��ĺ�������ʽΪS=�� ![]() x2+
x2+ ![]() x��0��x��4����
x��0��x��4����
�䷽�ã�S=�� ![]() ��x��2��2+
��x��2��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
��S�����ֵ��
��x=2ʱ��S�����ֵ�����ֵ�� ![]()
��3��
�⣺����ijһʱ�̣�ʹ��OMN��ֱ�������Σ��������£�
�����������������OMN=90�㣬��ͼ2��ʾ��

��MN��AB��
��ʱOM=4��x��ON=1.25x��
��MN��AB��
���OMN�ס�OAB��
�� ![]() ��
��
�� ![]() ��
��
��ã�x=2��
������ONM=90�㣬��ͼ3��ʾ��

���ONM=��OAB��
��ʱOM=4��x��ON=1.25x��
�ߡ�ONM=��OAB����MON=��BOA��
���OMN�ס�OBA��
�� ![]() ��
��
�� ![]() ��
��
��ã�x= ![]() ��
��
����������x��ֵ��2��� ![]() ��
��
����������1���ɹ��ɶ������OB����NP��OA��P����NP��AB���ó���OPN�ס�OAB���ó�����ʽ ![]() �����OP��PN�����ɵó���N�����ꣻ��2���������ε������ʽ�ó�S��x�Ķ��κ��������ɵó�S�����ֵ����3�������������������OMN=90�㣬��MN��AB����ƽ���ߵó���OMN�ס�OAB���ó�����ʽ���������x��ֵ��������ONM=90�㣬���ONM=��OAB��֤����OMN�ס�OBA���ó�����ʽ�����x��ֵ���ɣ�
�����OP��PN�����ɵó���N�����ꣻ��2���������ε������ʽ�ó�S��x�Ķ��κ��������ɵó�S�����ֵ����3�������������������OMN=90�㣬��MN��AB����ƽ���ߵó���OMN�ס�OAB���ó�����ʽ���������x��ֵ��������ONM=90�㣬���ONM=��OAB��֤����OMN�ס�OBA���ó�����ʽ�����x��ֵ���ɣ�
�����㾫�������ն��κ�������ֵ���ɶ����ĸ����ǽ����ĸ�������Ҫ֪������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a��ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
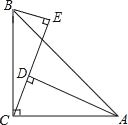
����Ŀ����ͼ����ACB=90����AC=BC��AD��CE��BE��CE������ֱ�ΪD��E��
��1��֤������BCE�ա�CAD��
��2����AD=25cm��BE=8cm����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ�ڡ��������չ�ë��ֱ�����ۣ�ÿ�ֿɻ���100Ԫ�����дּӹ���ÿ��ɼӹ�8�֣�ÿ�ֿɻ���800Ԫ�������ë����о��ӹ���ÿ��ɼӹ�1�֣�ÿ�ֿɻ���4000Ԫ���������������ƣ�ÿ��ֻ�ܲ���һ�ַ�ʽ�ӹ���Ҫ����һ���ڣ�30�죩������ë��93��ȫ�����ۣ�Ϊ����ҵ�����ټ�ְ�����ᣬ��ְ��������μӹ����۸����㣮
��˵����ë��ȫ�����дּӹ������ۣ�
��˵��30�춼���о��ӹ���δ�ӹ���ë��ֱ�����ۣ�
��˵��30���п��ü���ּӹ������ü��쾫�ӹ������ۣ�
���ʳ���Ӧ������λ˵�ķ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��F�ڶԽ���BD�ϣ���BF��DE��
����֤���ı���AECF�����Σ�
����AB��2��BF��1�����ı���AECF�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ�к졢�ơ���������ɫ������ɫ��ͬ�������ͬ�������к�����2����������1����������������1���Ǻ���ĸ���Ϊ ![]() ��
�� 
��1�������������ĸ�����
��2����1�δӴ�����������1���Żأ�����2������������1�������û���״ͼ���б���ķ����������ζ���������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOC��30�㣬��BOC��150�㣬ODΪ��BOA��ƽ���ߣ����DOC��90��.��A��ɱ�ʾΪ(2��30��)��B��ɱ�ʾΪ(4��150��)����D��ɱ�ʾΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ԼԪ����ɽ���ס������˾����ĸ߶�y(m)���ɽʱ��x(min)֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺
��1��t= min.
��2���������ٺ��ҵ�ɽ�������ٶ��Ǽ�ɽ�������ٶ�3����
�����ɽ�ĵ������ٶ��� m/min��
���������ɽ�����У������ĸ߶�y(m)���ɽʱ��x(min)֮��ĺ�����ϵʽ.
�����ס������˾����߶Ȳ�Ϊ70mʱ����x��ֵ��ֱ��д������������xֵ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��ABCD��,�ֱ���AB,ADΪ�߷ֱ��������ȱ�������ABE�͵ȱ�������ADF,�ӳ�CB��AE�ڵ�G,��G�ڵ�A,E֮��,����CE,CF,EF,�����н��۲�һ����ȷ����(����)

A. ��CDF�ա�EBC B. ��CDF=��EAF
C. ��ECF�ǵȱ������� D. CG��AE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ֱ������ϵ��������и���A��2��1����B��-2��1����C��3��2����D��-3��2����
��2������AB��CD�۲�������y��Ĺ�ϵ��
��3�����루a��1��(-a��1)����������Ƿ���ѭ��������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com