
 如图,△AP1B中,BP1⊥AP1,AP1=2,∠A=30°,P1Q1⊥AB,Q1P2⊥AP1,P2Q2⊥AB,Q2P3⊥AP1…,PnQn⊥AB,Pn+1Qn⊥AP1,则S=P1Q1+P2Q2+…+PnQn+…的值为
如图,△AP1B中,BP1⊥AP1,AP1=2,∠A=30°,P1Q1⊥AB,Q1P2⊥AP1,P2Q2⊥AB,Q2P3⊥AP1…,PnQn⊥AB,Pn+1Qn⊥AP1,则S=P1Q1+P2Q2+…+PnQn+…的值为 )2P1Q1=
)2P1Q1= P1Q1,得出一般规律,再求和.
P1Q1,得出一般规律,再求和. AP1=1,
AP1=1, P1Q1=
P1Q1= ,P3Q3=
,P3Q3= P2Q2=(
P2Q2=( )2,…,PnQn=(
)2,…,PnQn=( )n-1,
)n-1, +(
+( )2+…+(
)2+…+( )n-1+…,①
)n-1+…,① 得,
得, S=
S= +1+
+1+ +(
+( )2+…+(
)2+…+( )n-2+…,②
)n-2+…,② S-S=
S-S= -(
-( )n-1…,
)n-1…, )n-1接近0,此时,
)n-1接近0,此时, S-S=
S-S= ,
,

科目:初中数学 来源: 题型:
 如图,△AP1B中,BP1⊥AP1,AP1=2,∠A=30°,P1Q1⊥AB,Q1P2⊥AP1,P2Q2⊥AB,Q2P3⊥AP1…,PnQn⊥AB,Pn+1Qn⊥AP1,则S=P1Q1+P2Q2+…+PnQn+…的值为( )
如图,△AP1B中,BP1⊥AP1,AP1=2,∠A=30°,P1Q1⊥AB,Q1P2⊥AP1,P2Q2⊥AB,Q2P3⊥AP1…,PnQn⊥AB,Pn+1Qn⊥AP1,则S=P1Q1+P2Q2+…+PnQn+…的值为( )查看答案和解析>>
科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:059
数学探究课上李老师出了这样一道题:“如图,正三角形ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军一起讨论时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路.请按照下列思路要求画图或判断.
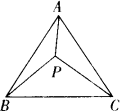
(1)在图中画出△APC绕A点顺时针旋转60°后的图形△AP1B;
(2)试判断△AP1P的形状,并说明理由;
(3)试判断△BP1P的形状,并说明理由;
(4)由2,3两问可知:∠APB=________.
李老师看过后,夸奖了他们,同时提示他们试试以B点或C点为旋转中点,对某个三角形进行适当地旋转,看一看是否可以求出∠APB度数.你认为可以吗?如果可以,给出一种具体的旋转方法;如果不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com