(1)解:∵AD⊥BC,DE⊥AC,
∴∠ADC=∠DEC=90°,又∠C=∠C,
∴△DEC∽△ADC,
∴

,
∴
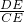
=
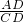
;
(2)解:∵∠ADC=∠DEC=90°,
∴∠ADM+∠EDC=90°,∠EDC+∠BCE=90°,

∴∠ADM=∠BCE,
又∵AB=AC,AD⊥BC,
∴D为BC的中点,即BD=CD=

BC,
∵M为DE的中点,
∴DM=EM=

DE,
由(1)得
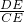
=
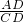
,
∴

,
∴

,
∴△BCE∽△ADM.
分析:(1)由AD与BC垂直,DE与AC垂直,利用垂直的定义得到一对直角相等,再由一对公共角,利用两对对应角相等的两三角形相似得到△DEC∽△ADC,根据相似三角形的对应边成比例得到比例式,变形后即可得证;
(2)由三角形ADC与三角形DEC都为直角三角形,利用同角的余角相等得出一对角相等,根据M为中点,得到DE=2DM,AB=AC且AD⊥BC,利用三线合一得到D为BC的中点,可得出CD=

BC,代入(1)得出的比例式中,变形后得到两对对应边相等,利用两对对应边且夹角相等的两三角形相似可得证.
点评:此题考查了相似三角形的判定与性质,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;两边对应成比例且夹角相等的两三角形相似;三边对应成比例的两三角形相似,本题第二问用的是第二种方法.

 如图,在△ABC中,AB=AC,AD⊥BC,DE⊥AC,M为DE的中点,AM与BE相交于N,AD与BE相交于F.
如图,在△ABC中,AB=AC,AD⊥BC,DE⊥AC,M为DE的中点,AM与BE相交于N,AD与BE相交于F.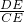 =
=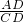 ;
;  ,
,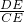 =
=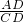 ;
;
 BC,
BC, DE,
DE,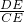 =
=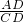 ,
, ,
, ,
, BC,代入(1)得出的比例式中,变形后得到两对对应边相等,利用两对对应边且夹角相等的两三角形相似可得证.
BC,代入(1)得出的比例式中,变形后得到两对对应边相等,利用两对对应边且夹角相等的两三角形相似可得证.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为