
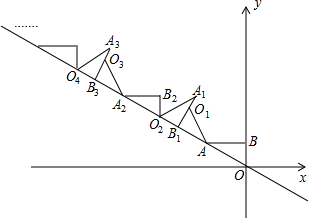
 如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.
如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$. 分析 观察图象可知,O12在直线y=-$\frac{\sqrt{3}}{3}$x时,OO12=6•OO2=6(1+$\sqrt{3}$+2)=18+6$\sqrt{3}$,由此即可解决问题.
解答 解:观察图象可知,O12在直线y=-$\frac{\sqrt{3}}{3}$x时,
OO12=6•OO2=6(1+$\sqrt{3}$+2)=18+6$\sqrt{3}$,
∴O12的横坐标=-(18+6$\sqrt{3}$)•cos30°=-9-9$\sqrt{3}$,
O12的纵坐标=$\frac{1}{2}$OO12=9+3$\sqrt{3}$,
故答案为9+3$\sqrt{3}$.
点评 本题考查坐标与图形的变化、规律型:点的坐标、一次函数的性质等知识,解题的关键是学会从特殊到一般的探究方法,属于中考常考题型.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
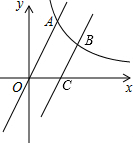 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
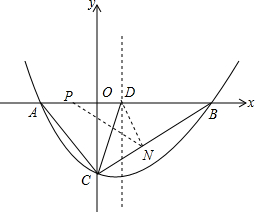 已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com