
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:AC2=ADAB;
(2)求证:AC2+BC2=AB2(即证明勾股定理);
(3)如果AC=4,BC=9,求AD:DB的值;
(4)如果AD=4,DB=9,求AC:BC的值.

【答案】(1)见解析;(2)见解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)欲证明AC2=ADAB,只要证明△ACD∽△ABC;
(2)同理可证BC2=BDAB,由AC2=ADAB.推出AC2+BC2=ADAB+BDAB=AB2;
(3)由BC2=BDAB,AC2=ADAB,推出![]() =
=![]() ,即
,即![]() =
=![]() ,由此即可计算;
,由此即可计算;
(4)用类似(3)的方法计算即可.
(1)∵CD⊥AB,∠ACB=90°,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
∴![]() ,
,
∴AC2=ADAB;
(2)同理可证BC2=BDAB,
∵AC2=ADAB.
∴AC2+BC2=ADAB+BDAB=AB2,
∴AC2+BC2=AB2;
(3)∵BC2=BDAB,AC2=ADAB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
(4)∵BC2=BDAB,AC2=ADAB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
(1)图象的另一支位于什么象限?常数n的取值范围是什么?
(2)试比较a、b的大小;
(3)作AC⊥x轴于点C,若△AOC的面积为5,求这个反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个工人拿一个![]() 米长的梯子,底端
米长的梯子,底端![]() 放在距离墙根
放在距离墙根![]() 点
点![]() 米处,另一端点
米处,另一端点![]() 点靠墙.
点靠墙.
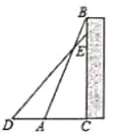
(1)求这个梯子的顶端距离地面的高度![]() ;
;
(2)如图,如果梯子的顶部下滑![]() 米,那么梯子的底部向外滑多少米.
米,那么梯子的底部向外滑多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚在实践课上要做一个如图1所示的折扇,折扇扇面的宽度AB是骨柄长OA的![]() ,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24
,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24![]() cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )

A. 21cm B.20 cm C. 19cm D. 18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市初中学生每天进行体育锻炼的时间,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
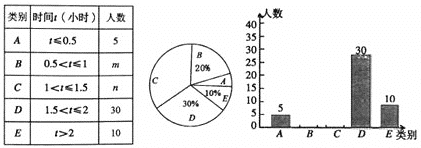
请根据图表信息解答下列问题:
(1)在统计表中,m=_______,n=____,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是_______;
(3)据了解该市大约有3万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的三张形状相同、大小完全相同的方格纸,方格纸中每个小正方形的边长为1,请依次在3个图中画出满足要求的三角形,要求所画的三角形的各顶点必须与方格纸中小正方形的顶点重合.
(1)画一个底边长为4,面积为10的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个一边长为2![]() 且面积为10的等腰三角形.
且面积为10的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
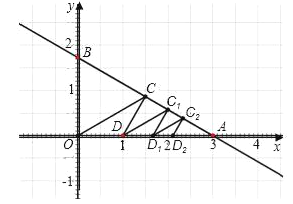
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com